题目内容
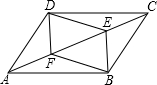 平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF.
平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF.(1)求证:△AFD≌△CEB;
(2)求证:四边形BFDE是平行四边形.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用“平行四边形的对边相等且平行的性质”推知BC=AD,BC∥AD.所以由平行线的性质得到∠DAF=∠BCE,结合已知条件∠ADF=∠CBE,易证得
△AFD≌△CEB(ASA);
(2)由“由一组对边相等且平行是四边形为平行四边形”证得结论.
△AFD≌△CEB(ASA);
(2)由“由一组对边相等且平行是四边形为平行四边形”证得结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∴∠DAF=∠BCE,
∵∠ADF=∠CBE,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(ASA);
(2)∵由(1)知,△AFD≌△CEB,
∴DF=BE,
∴∠AFD=∠CBE,
∴∠DFE=∠BEF,
∴DF∥BE,
∴四边形BFDE是平行四边形.(方法不唯一)
∴BC=AD,BC∥AD,
∴∠DAF=∠BCE,
∵∠ADF=∠CBE,
在△AFD和△CEB中,
|
∴△AFD≌△CEB(ASA);
(2)∵由(1)知,△AFD≌△CEB,
∴DF=BE,
∴∠AFD=∠CBE,
∴∠DFE=∠BEF,
∴DF∥BE,
∴四边形BFDE是平行四边形.(方法不唯一)
点评:本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
反比例函数y=-
与正比例函数y=kx的一个交点为(-1,2),则关于x的方程-
=kx的解为( )
| 2 |
| x |
| 2 |
| x |
| A、x1=-1,x2=1 |
| B、x1=-1,x2=2 |
| C、x1=-2,x2=1 |
| D、x1=-1,x2=-2 |
 如图,已知二次函数y=ax2+bx-
如图,已知二次函数y=ax2+bx- 如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F.
如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F. 如图,AB∥DC,∠ABD=30°,∠ADB=85°,求∠ADC和∠A的角度.
如图,AB∥DC,∠ABD=30°,∠ADB=85°,求∠ADC和∠A的角度.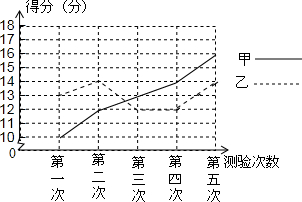 甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示
甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示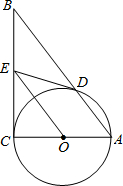 如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E. 如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.
如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.