Question

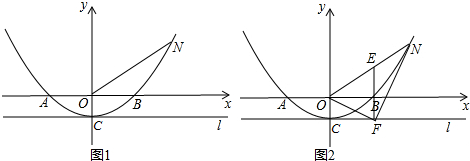
如图，抛物线C₁：y=ax²+bx+4的图象与两坐标轴分别交于A、B、C三点，经过点E（0，-2）的直线l：y=kx-2（k≠0）与x轴、抛物线的对称轴x=-1交于点F．
（1）填空：OC=

 

；OF=

 

；
（2）连结AE．若△OAE∽△OEF，请求出抛物线C₁的解析式；
（3）在（2）的条件下，把抛物线C₁向右平移1个单位后，向下平移

9

2

个单位得到新的抛物线C₂．再将直线l绕着点E进行旋转，当直线l与抛物线C₂相交于不同的两个交点M、N时，过点P（0，2）、点M与点N分别作直线PM、PN．猜想：直线PM、PN、CE之间的位置关系（除相交于点P外）．并请说明理由．

Answer 1

考点：二次函数综合题

专题：

分析：（1）利用图象上点的坐标性质得出CO，FO的长；
（2）利用相似三角形的性质得出AO的长，进而利用待定系数法求出二次函数解析式；
（3）根据题意分别表示出M，N点的坐标，进而得出tan∠MPG=tan∠NPH，进而得出答案．

解答：解：（1）∵y=ax²+bx+4的图象与两坐标轴分别交于A、B、C三点，
∴x=0时，y=4，
∴CO=4，
∵y=kx-2（k≠0）与x轴、抛物线的对称轴x=-1交于点F，
∴FO=1，
故答案为：4；1；

（2）∵E（0，-2），y=kx-2（k≠0）与抛物线的对称轴x=-1交于点F，
∴OE=2，OF=1．
∵△OAE∽△OEF，

OA

OE

=

OE

OF

，
∴OA=4
即A（-4，0），B（2，0），
代入y=ax²+bx+4可得：

16a-4b+4=0 4a+2b+4=0

，
解得：

a=- 1 2 b=-1

，
故抛物线C₁的解析式为：y=-

1

2

x2-x+4；

（3）直线PM、PN关于直线CE成轴对称．
或直线PM、与直线CE、直线PN与直线CE的夹角相等（相类似的也行），
过点N作NH⊥y轴于点H，过点M作MG⊥y轴于点G，
 y=-

1

2

x2-x+4=-

1

2

(x+1)2+

9

2

故抛物线C₂的解析式为y=-

1

2

x2，
由点M、N在直线l和抛物线C₂的图象上得：kx-2=-

1

2

x2
解得x1=-k-

k2+4

，x2=-k+

k2+4

，
当x1=-k-

k2+4

时，y1=-k2-2+

k2+4

，
当x2=-k+

k2+4

时，y2=-k2-2-

k2+4

，
故M(-k-

k2+4

，-k2-2+

k2+4

)，N(-k+

k2+4

，-k2-2-

k2+4

)
则tan∠MPG=

MG

PG

=

k+ k2+4

2-(-k2-2+ k2+4 )

=

1

k2+4

tan∠NPH=

NH

PH

=

-k+ k2+4

2-(-k2-2- k2+4 )

=

1

k2+4

，
故tan∠MPG=tan∠NPH，
即∠MPG=∠NPH，
综上所述：直线PM、PN关于直线CE成轴对称．

点评：此题主要考查了二次函数综合应用以及相似三角形的性质和锐角三角函数关系等知识，分别表示出M，N点坐标是解题关键．