题目内容
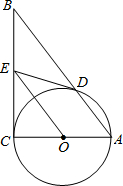 如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长;
(3)在(2)的条件下,求△ADO的面积.
考点:切线的判定,勾股定理
专题:
分析:(1)连OD,首先证明△EOC≌△EOD,则可以证得∠EDO=∠ECO=90°,即可证得;
(2)证明OE是△ABC的中位线,在直角△OEC中,利用勾股定理求得OE的长,然后利用三角形中位线定理求得AB的长;
(3)连接CD,则CD是直角△ABC的斜边AB上的高,根据三角形的面积公式即可求得CD的长,则在直角△ACD中,利用勾股定理求得AD的长,则△ACD的面积即可求得,进而求得△ADO的面积.
(2)证明OE是△ABC的中位线,在直角△OEC中,利用勾股定理求得OE的长,然后利用三角形中位线定理求得AB的长;
(3)连接CD,则CD是直角△ABC的斜边AB上的高,根据三角形的面积公式即可求得CD的长,则在直角△ACD中,利用勾股定理求得AD的长,则△ACD的面积即可求得,进而求得△ADO的面积.
解答: (1)证明:连OD,
(1)证明:连OD,
∵OE∥AB,
∴∠EOC=∠A,∠EOD=∠ODA,
又∵OA=OD,
∴∠A=∠ODA,
∴∠EOC=∠EOD,
在△EOC和△EOD中,
,
∴△EOC≌△EOD(SAS),
∴∠EDO=∠ECO,
又∵∠C=90°,
∴∠EDO=90°即ED⊥DO 而点D在⊙O上,
∴ED为⊙O的切线.
(2)∵OE∥AB,OA=OC
∴AB=2OE
又∵∠C=90°,
∴OC⊥EC,
∴EC是⊙O的切线.
∴EC=ED=2,
在△OCE中,OE=
=
=2.5,
∴AB=2OE=5;
(3)连结CD.
∵AC是⊙O的直径,
∴∠CDA=90°
∴CD⊥AB
在Rt△ABC中,CD⊥AB,
∴CD•AB=AC•BC,
∴CD=2.4,
在Rt△ACD中,AD=
=
=1.8,
∴S△ACD=
CD•AD=2.16,
∴S△ADO=
S△ACD=1.08.
 (1)证明:连OD,
(1)证明:连OD,∵OE∥AB,
∴∠EOC=∠A,∠EOD=∠ODA,
又∵OA=OD,
∴∠A=∠ODA,
∴∠EOC=∠EOD,
在△EOC和△EOD中,
|
∴△EOC≌△EOD(SAS),
∴∠EDO=∠ECO,
又∵∠C=90°,
∴∠EDO=90°即ED⊥DO 而点D在⊙O上,
∴ED为⊙O的切线.
(2)∵OE∥AB,OA=OC
∴AB=2OE
又∵∠C=90°,
∴OC⊥EC,
∴EC是⊙O的切线.
∴EC=ED=2,
在△OCE中,OE=
| OC2+CE2 |
| 1.52+22 |
∴AB=2OE=5;
(3)连结CD.
∵AC是⊙O的直径,
∴∠CDA=90°
∴CD⊥AB
在Rt△ABC中,CD⊥AB,
∴CD•AB=AC•BC,
∴CD=2.4,
在Rt△ACD中,AD=
| AC2-CD2 |
| 32-2.42 |
∴S△ACD=
| 1 |
| 2 |
∴S△ADO=
| 1 |
| 2 |
点评:本题考查切线的判定以及勾股定理,已知所证的直线经过圆上的点,证切线常用的方法是转化成证垂直.

练习册系列答案
相关题目
 如图,直线AB、CD相交于O,OE是∠AOD的角平分线,∠AOC=28°,求∠AOE的度数.
如图,直线AB、CD相交于O,OE是∠AOD的角平分线,∠AOC=28°,求∠AOE的度数.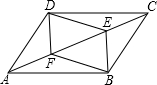 平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF.
平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF. 如图,顶点为A(1,4)的抛物线与y轴交于点B(0,2),与x轴交于C,D两点,抛物线上一动点P沿抛物线从点C向点A运动,点P关于抛物线对称轴的对称点为点Q,分别过点P,Q向x轴作垂线,垂足分别为点M,N.抛物线对称轴与x轴相交于点E.
如图,顶点为A(1,4)的抛物线与y轴交于点B(0,2),与x轴交于C,D两点,抛物线上一动点P沿抛物线从点C向点A运动,点P关于抛物线对称轴的对称点为点Q,分别过点P,Q向x轴作垂线,垂足分别为点M,N.抛物线对称轴与x轴相交于点E.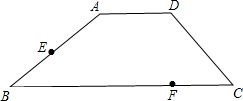 如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.
如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.
 如图,直线l与直线AB、CD分别相交于E、F,∠1=105°,当∠2=
如图,直线l与直线AB、CD分别相交于E、F,∠1=105°,当∠2=