题目内容
2．解分式方程：-$\frac{x-3}{x}-2=\frac{3x}{x-3}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：去分母得：-（x-3）2-2x（x-3）=3x2，
整理得：-x2+6x-9-2x2+6x=3x2，即2x2+6x+3=0，
解得：x=$\frac{-6±2\sqrt{3}}{4}$=$\frac{-3±\sqrt{3}}{2}$，
经检验x=$\frac{-3±\sqrt{3}}{2}$都为分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
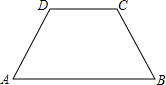如图所示，AB∥DC，AD=DC=BC，∠A=∠B=60°．你能把它分成三个全等的三角形吗？你能把它分成四个全等的四边形吗？试一试．
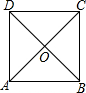如图，正方形的边长为2，中心为O，从O、A、B、C、D五点中任取两点．
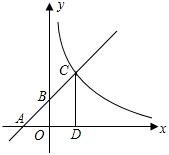如图，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=$\frac{m}{x}$（x＞0）的图象在第一象限相交于点C，CD垂直于x轴，垂足为点D，若OA=OB=2，OD=1．
7．甲、乙、丙、丁四位同学五次数学测验成绩统计如下表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加上海市初中数学竞赛，那么应选乙同学．
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 70 | 85 | 85 | 70 |
| 标准差 | 6.5 | 6.5 | 7.6 | 7.6 |