题目内容
10.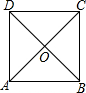 如图,正方形的边长为2,中心为O,从O、A、B、C、D五点中任取两点.
如图,正方形的边长为2,中心为O,从O、A、B、C、D五点中任取两点.(1)求取到的两点间的距离为2的概率;
(2)求取到的两点间的距离为$2\sqrt{2}$的概率;
(3)求取到的两点间的距离为$\sqrt{2}$的概率.
分析 (1)先求出两点间的距离为2的所有情况,再根据概率公式除以总的情况数即可;
(2)先求出两点间的距离为2$\sqrt{2}$的所有情况,再根据概率公式计算即可;
(3)先求出两点间的距离为$\sqrt{2}$的所有情况,再根据概率公式进行计算即可;
解答 解:(1)从O、A、B、C、D五点中任取两点,所有等可能出现的结果有:
AB、AC、AD、BC、BD、CD、OA、OB、OC、OD,共有10种,
满足两点间的距离为2的结果有AB、BC、CD、AD这4种,
则P(两点间的距离为2)=$\frac{4}{10}$=$\frac{2}{5}$.
(2)满足两点间的距离为$2\sqrt{2}$的结果有AC、BD这2种.
则P(两点间的距离为$2\sqrt{2}$)=$\frac{2}{10}$=$\frac{1}{5}$.
(3)满足两点间的距离为$\sqrt{2}$的结果有OA、OB、OC、OD这4种.
则P(两点间的距离为$\sqrt{2}$)=$\frac{4}{10}$=$\frac{2}{5}$.
点评 此题考查了几何概率,掌握概率公式,利用列举法求出所有符合条件的情况数是解决本题的关键.

练习册系列答案
相关题目
18.若将抛物线y=$\frac{1}{2}$x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的表达式是( )
| A. | $y=\frac{1}{2}{(x+2)^2}-1$ | B. | $y=\frac{1}{2}{(x-2)^2}-1$ | C. | y=(x+2)2-1 | D. | $y=\frac{1}{2}(x-2)+1$ |
18.下表为宁波市2016年4月上旬10天的日最低气温情况,则这10天中日最低气温的中位数和众数分别是( )
| 温度(℃) | 11 | 13 | 14 | 15 | 16 |
| 天数 | 1 | 5 | 2 | 1 | 1 |
| A. | 14℃,14℃ | B. | 14℃,13℃ | C. | 13℃,13℃ | D. | 13℃,14℃ |
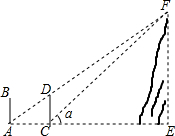 如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)
如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)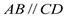 ② AB=CD ③
② AB=CD ③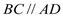 ④BC=AD这四个条件中任意选两个,能使四边形ABCD是平行四边形的选法有______种
④BC=AD这四个条件中任意选两个,能使四边形ABCD是平行四边形的选法有______种