题目内容
9.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-3y=1}\\{x+by=5}\end{array}\right.$ 的解,求α的值.【思路探究】:(1)$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ 是方程ax-3y=1的解吗?
(2)根据二元一次方程的解的定义,由结论(1)能列出关于a的方程吗?
(3)$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ 是方程x+by=5的解吗?
分析 (1)根据二元一次方程组的两个方程的公共解是二元一次方程组的解,可得答案;
(2)根据二元一次方程的解满足方程,可得关于a的一元一次方程,根据解方程,可得答案;
(3)根据二元一次方程组的两个方程的公共解是二元一次方程组的解,可得答案.
解答 解:(1)由$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-3y=1}\\{x+by=5}\end{array}\right.$ 的解,得
$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ 是方程ax-3y=1的解;
(2)由$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ 是方程ax-3y=1的解,得
2a-3=1,
解得a=2.
(3)由$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-3y=1}\\{x+by=5}\end{array}\right.$ 的解,得
$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ 是方程x+by=5的解.
点评 本题考查了二元一次方程组的解,利用方程组的解满足方程的出关于a的方程是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下表为宁波市2016年4月上旬10天的日最低气温情况,则这10天中日最低气温的中位数和众数分别是( )
| 温度(℃) | 11 | 13 | 14 | 15 | 16 |
| 天数 | 1 | 5 | 2 | 1 | 1 |
| A. | 14℃,14℃ | B. | 14℃,13℃ | C. | 13℃,13℃ | D. | 13℃,14℃ |
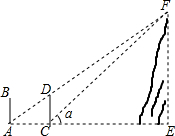 如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)
如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)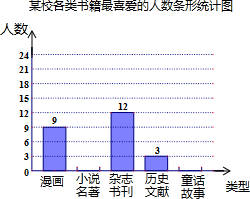 李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的$\frac{5}{7}$,请完成下列问题:
李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的$\frac{5}{7}$,请完成下列问题: 如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.
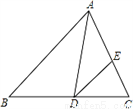
如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.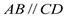 ② AB=CD ③
② AB=CD ③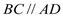 ④BC=AD这四个条件中任意选两个,能使四边形ABCD是平行四边形的选法有______种
④BC=AD这四个条件中任意选两个,能使四边形ABCD是平行四边形的选法有______种