题目内容
17.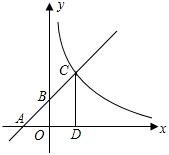 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(x>0)的图象在第一象限相交于点C,CD垂直于x轴,垂足为点D,若OA=OB=2,OD=1.
如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(x>0)的图象在第一象限相交于点C,CD垂直于x轴,垂足为点D,若OA=OB=2,OD=1.(1)直接写出A、B、D三点的坐标;
(2)求一次函数和反比例函数的解析式.
分析 (1)根据原点到A、B、D三点的距离结合图形中A、B、D三点的位置,即可得出三点的坐标;
(2)由A、B点在一次函数图象上,用待定系数法即可求出一次函数解析式,由CD⊥x轴,可知C、D点的横坐标相等,由点C在一次函数图象上,可求出点C的坐标,再将C点坐标代入反比例函数解析式,可得出关于m的方程,解方程即可得出m的值,从而得出反比例函数解析式.
解答 解:(1)∵OA=OB=2,OD=1,A点在x轴负半轴,B在y轴正半轴,D在x轴正半轴,
∴点A(-2,0),B(0,2),D(1,0).
(2)将点A、B的坐标代入y=kx+b中得:
$\left\{\begin{array}{l}{0=-2k+b}\\{2=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$.
∴一次函数的解析为为y=kx+2.
∵CD垂直于x轴,点D坐标为(1,0),
∴点C的坐标为(1,3).
∵点C(1,3)在反比例函数y=$\frac{m}{x}$的图象上,
∴有3=$\frac{m}{1}$,即m=3.
∴反比例函数的解析式为y=$\frac{3}{x}$(x>0).
点评 本题考查了反比例函数与一次函数的交点问题以及待定系数法求函数解析式,解题的关键是:(1)根据点的位置确定坐标;(2)利用待定系数法求函数解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标,利用待定系数法求出函数解析式是关键.

练习册系列答案
相关题目
8.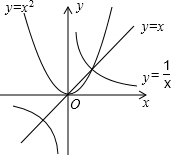 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
| A. | 正确的命题是①② | B. | 错误的命题是②③④ | C. | 正确的命题是①④ | D. | 错误的命题只有③ |
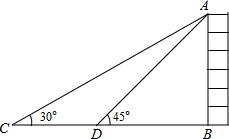 如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).
如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).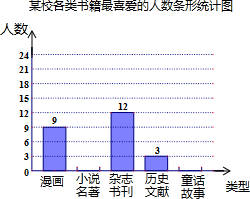 李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的$\frac{5}{7}$,请完成下列问题:
李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的$\frac{5}{7}$,请完成下列问题: