题目内容
12．
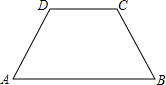如图所示，AB∥DC，AD=DC=BC，∠A=∠B=60°．你能把它分成三个全等的三角形吗？你能把它分成四个全等的四边形吗？试一试．
分析 过点D作DO∥BC交AB于O，连接OC，如图1，易证△ADO、△DOC、△BOC都是等边三角形，因而这三个三角形全等；由图1可得AB=2AD=2DC=2BC，只需分别以AD、DC、BC为底作与原四边形相似的四边形，就可解决问题．
解答 解：过点D作DO∥BC交AB于O，连接OC，如图1，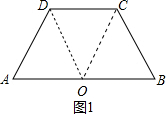
则△ADO、△DOC、△BOC即为所求作；
在线段AB上取两点G、H，使得AG=BH=$\frac{1}{4}$AB，
过点D、G分别作BC、AD的平行线交于点E，
过点C、H分别作AD、BC的平行线交于点F，连接EF，如图2，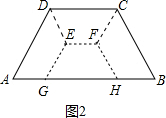
则四边形AGED、四边形GEFH、四边形BHFC、四边形CFED即为所求作．
点评 本题是一道作图题，既考查了操作能力，又考查了分析问题和解决问题的能力．
练习册系列答案
相关题目
如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．
4．
某超市举行购物“翻牌抽奖”活动，如图所示，四张牌分别对应价值5，10，15，20（单位：元）的四件奖品，如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总价值不低于30元的概率为（ ）
某超市举行购物“翻牌抽奖”活动，如图所示，四张牌分别对应价值5，10，15，20（单位：元）的四件奖品，如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总价值不低于30元的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{4}$ |
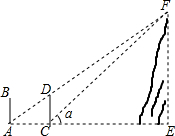如图，相邻两输电杆AB、CD相距100m，高度都为20m，驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上，小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°，求山顶F的高．（精确到0.1m）