题目内容
13.先化简,再求值:($\frac{3x}{x+2}$-$\frac{x}{x-2}$)÷$\frac{2x}{{x}^{2}-4}$,其中x=4-$\sqrt{3}$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{3x(x-2)-x(x+2)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$
=$\frac{3{x}^{2}-6x-{x}^{2}-2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$
=$\frac{2x(x-4)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$
=x-4,
当x=4-$\sqrt{3}$时,原式=4-$\sqrt{3}$-4=-$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
4. 某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
 某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
8.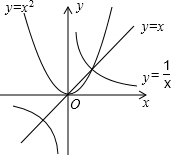 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
| A. | 正确的命题是①② | B. | 错误的命题是②③④ | C. | 正确的命题是①④ | D. | 错误的命题只有③ |
18.若将抛物线y=$\frac{1}{2}$x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的表达式是( )
| A. | $y=\frac{1}{2}{(x+2)^2}-1$ | B. | $y=\frac{1}{2}{(x-2)^2}-1$ | C. | y=(x+2)2-1 | D. | $y=\frac{1}{2}(x-2)+1$ |
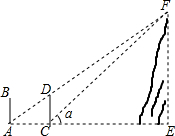 如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)
如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m) 如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.
如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于不同的两点A(x1,x2),B(x2,y2),与x轴交于点P(x0,0),与y轴交于点C.