题目内容
1. 如图,在△ABC中,∠A=90°.
如图,在△ABC中,∠A=90°.(1)用直尺和圆规作出BC的垂直平分线(保留作图痕迹,不要求写作法);
(2)BC的垂直平分线与AC相交于D,连结BD,若∠C=30°,则∠ABD=30°.
分析 (1)分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径化弧,两弧交于两点,再过两点作直线即可;
(2)根据直角三角形两锐角互余可得∠ABC=60°,然后再根据线段垂直平分线的性质可得BD=CD,进而可得∠C=∠DBC=30°,再根据角的和差关系可得答案.
解答 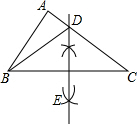 解:(1)如图所示,
解:(1)如图所示,
(2)∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵DE是BC的垂直平分线,
∴BD=CD,
∴∠C=∠DBC=30°,
∴∠ABD=60°-30°=30°,
故答案为:30°.
点评 此题主要考查了基本作图,以及线段垂直平分线的性质,关键是掌握线段垂直平分线的做法,线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
9.用配方法解方程x2-2x-8=0,下列配方结果正确的是( )
| A. | (x+1)2=9 | B. | (x+1)2=7 | C. | (x-1)2=9 | D. | (x-1)2=7 |
16.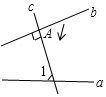 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )| A. | 20° | B. | 30° | C. | 50° | D. | 70° |
 如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是2.
如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是2.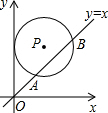 如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.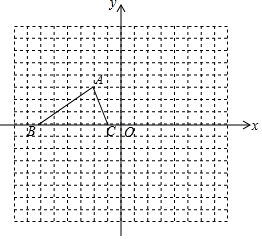 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).