题目内容
6.设y=(2n+1)x${\;}^{{n}^{2}+n-1}$(1)当n为何值时,y与x是正比例函数,且图象经过一、三象限;
(2)当n为何值时,y与x是反比例函数,且在每个象限内y随着x的增大而增大.
分析 (1)根据正比例函数的定义结合正比例函数的性质即可得出关于n的一元一次不等式以及一元二次方程,解之即可得出结论;
(2)根据反比例函数的定义结合反比例函数的性质即可得出关于n的一元一次不等式以及一元二次方程,解之即可得出结论.
解答 解:(1)∵y与x是正比例函数,且图象经过一、三象限,
∴$\left\{\begin{array}{l}{2n+1>0}\\{{n}^{2}+n-1=1}\end{array}\right.$,解得:n=1,
∴当n为1时,y与x是正比例函数,且图象经过一、三象限;
(2)∵y与x是反比例函数,且在每个象限内y随着x的增大而增大,
∴$\left\{\begin{array}{l}{2n+1<0}\\{{n}^{2}+n-1=-1}\end{array}\right.$,解得:n=-1,
∴当n为-1时,y与x是反比例函数,且在每个象限内y随着x的增大而增大.
点评 本题考查了正比例函数的定义、正比例函数的性质、反比例函数的定义以及反比例函数的性质,熟练掌握正、反比例函数的性质是解题的关键.

练习册系列答案
相关题目
14.下列算式中,结果是x6的是( )
| A. | x3•x2 | B. | x12÷x2 | C. | (x2)3 | D. | 2x6+3x6 |
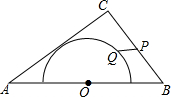 如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5.
如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5. 如图,在△ABC中,∠A=90°.
如图,在△ABC中,∠A=90°.
 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=4,则△BCE的面积等于( )
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=4,则△BCE的面积等于( )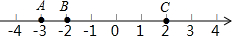 如图,在数轴上有三个点A、B、C,回答下列问题.
如图,在数轴上有三个点A、B、C,回答下列问题.