Question

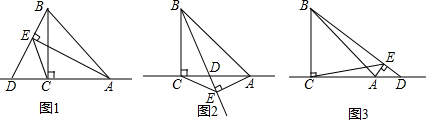
9．已知，在△ABC中，∠ACB=90°，CA=CB，D是直线AC上一点，连接BD，作AE⊥BD，垂足为E，连接EC．
（1）如图1，D在AC延长线上，AC＞CD，求证：EA-EB=$\sqrt{2}$EC；
（2）当D在AC上（图2）或D在CA延长线上（图3）时，EA、EB、EC三条线段的数量关系如何？直接写出你探究的结论．

Answer 1

分析 （1）在AE上截取AF=EB，连接CF，如图1，利用等角的余角相等得到∠DAE=∠DBC，则可根据“SAS”判断△EBC≌△FAC，得到EC=FC，∠BCE=∠ACF，再证明∠ECF=90°，于是可判断△CEF为等腰直角三角形，得到EF=$\sqrt{2}$CE，所以EA-EB=EA-AF=EF=$\sqrt{2}$EC，
（2）当D在AC上（图2）时，在BE上截取BF=EA，连接CF，同样方法可得△FBC≌△EA得到FC=EC，∠BCF=∠ACE，再证明△CEF为等腰直角三角形，则EF=$\sqrt{2}$CE，所以EB-EA=EB-BF=EF=$\sqrt{2}$EC；当 D在CA延长线上（图3）时，在BE的反向延长线上截取BF=EA，连接CF，同样方法可得△FBC≌△EAC得到FC=EC，同样可得EF=$\sqrt{2}$CE，则EA+EA=FB+EB=EF=$\sqrt{2}$EC，

解答 （1）证明：在AE上截取AF=EB，连接CF，如图1，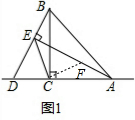
∵AE⊥BD，
∴∠AEB=90°，
∴∠AEB=∠ACB=90°，
又∵∠DAE+∠ADE=90°，∠BDC+∠DBC=90°，
∴∠DAE=∠DBC，
在△EBC和△FAC中，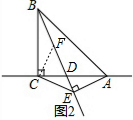
$\left\{\begin{array}{l}{BE=AF}\\{∠EBC=∠FAC}\\{BC=AC}\end{array}\right.$，
∴△EBC≌△FAC（SAS），
∴EC=FC，∠BCE=∠ACF，
∴∠ECF=∠BCE+∠GCF=∠ACF+∠GCF=∠ACB=90°，
∴△CEF为等腰直角三角形，
∴EF=$\sqrt{2}$CE，
∴EA-EB=EA-AF=EF=$\sqrt{2}$EC，
即EA-EB=$\sqrt{2}$EC；
（2）当D在AC上（图2）时，在BE上截取BF=EA，连接CF，
同样方法可得△FBC≌△EAC（SAS），则FC=EC，∠BCF=∠ACE，
∴∠ECF=∠ACB=90°，
∴△CEF为等腰直角三角形，
∴EF=$\sqrt{2}$CE，
∴EB-EA=EB-BF=EF=$\sqrt{2}$EC，
即EB-EA=$\sqrt{2}$EC；
当 D在CA延长线上（图3）时，在BE的反向延长线上截取BF=EA，连接CF，
同样方法可得△FBC≌△EAC（SAS），则FC=EC，∠BCF=∠ACE，
∴∠ECF=∠ACB=90°，
∴△CEF为等腰直角三角形，
∴EF=$\sqrt{2}$CE，
∴EA+EA=FB+EB=EF=$\sqrt{2}$EC，
即EA+EB=$\sqrt{2}$EC．

点评 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了等腰直角三角形的判定与性质．