题目内容
17.小明和小颖做掷骰子的游戏,规则如下:①游戏前每人选一个数字;②每次同时掷两枚均匀骰子;③如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.(1)用列表法或树状图列出同时掷两枚均匀骰子所有可能出现的结果;
(2)已知小明选的数字是5,小颖选的数字是6.如果你也加入游戏,你会选什么数字,才能使自己获胜的概率比他们大?请说明理由.
分析 (1)列表将所有等可能的结果列举出来即可;
(2)分别求得概率,然后比较大小即可确定谁获胜的概率大.
解答 解:(1)列表法或树状图:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
∴我会选数字7.
点评 本题考查借助树状图或列表法求概率.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
8.为了调查参加运动会1000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是( )
| A. | 1000名运动员是总体 | B. | 抽取的100名运动员是样本 | ||
| C. | 样本容量是100 | D. | 每个运动员是个体 |
12.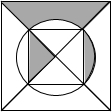 在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
 在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
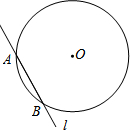 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A逆时针旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为$\frac{π}{2}$$+\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A逆时针旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为$\frac{π}{2}$$+\frac{\sqrt{3}}{2}$.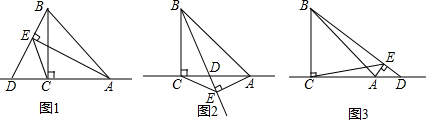
 如图,在正方形ABCD中,E、F分别为AB、BC上的点,且AE=BF,连结DE、AF,猜想DE、AF的关系并证明.
如图,在正方形ABCD中,E、F分别为AB、BC上的点,且AE=BF,连结DE、AF,猜想DE、AF的关系并证明.