题目内容
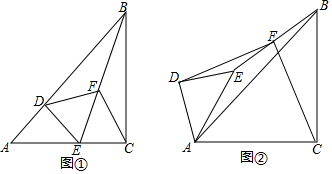
18. 如图,直角梯形ABCD中,∠A=∠B=∠DEC=90°,E为AB中点,求证:AD+BC=DC.
如图,直角梯形ABCD中,∠A=∠B=∠DEC=90°,E为AB中点,求证:AD+BC=DC.
分析 延长DE,CB交于F,根据ASA证明△DEA≌△FEB得AD=BF,DE=FE,再根据线段垂直平分线的性质可得CF=CD,根据等量关系即可证明AD+BC=DC.
解答  解:延长DE,CB交于F,
解:延长DE,CB交于F,
∵∠A=∠B=90°,
∴∠A=∠EBF=90°,
∵E为AB中点,
∴AE=BE,
在△DEA与△FEB中,
$\left\{\begin{array}{l}{∠A=∠EBF}\\{AE=BE}\\{∠AED=∠BEF}\end{array}\right.$,
∴△DEA≌△FEB(ASA),
∴AD=BF,DE=FE,
∵∠DEC=90°,
∴CF=CD,
∴AD+BC=BF+BC=CF=DC.
点评 本题考查直角梯形的性质、全等三角形的判定与性质以及线段垂直平分线的性质,添加辅助线证明全等是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6.已知一个物体的高度为$\sqrt{55}$cm,则这个物体可能是( )
| A. | 火柴盒 | B. | 粉笔盒 | C. | 书桌 | D. | 旗杆 |
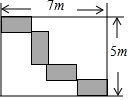 如图是某居民小区内的矩形工地,工地里有四块相同的小矩形绿化区域.小矩形的边都与工地的边平行,每个矩形由顶点连接,求小矩形的长和宽.
如图是某居民小区内的矩形工地,工地里有四块相同的小矩形绿化区域.小矩形的边都与工地的边平行,每个矩形由顶点连接,求小矩形的长和宽.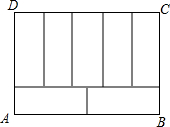 如图,周长为68cm的长方形ABCD被分成7个相同的矩形,求长方形ABCD的面积.
如图,周长为68cm的长方形ABCD被分成7个相同的矩形,求长方形ABCD的面积.