题目内容
13.如图.已知P为线段AB上一点,M、N分别是AP、BP中点.
(1)若AP=6,BP=4,则AB=10,MN=5;
(2)若AB=16,AP=10,MN=8;
(3)若AB=18,则MN=9;
(4)若AB=a,则MN=$\frac{1}{2}$a.
分析 (1)首先根据中点定义可得到AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,再根据图形可得MN=MP+PN,即可得到答案;
(2)先求得PB,再根据中点定义可得到AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,再根据图形可得MN=MP+PN,即可得到答案;
(3)根据中点定义可得到AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,再根据图形可得MN=MP+PN,即可得到答案;
(4)根据中点定义可得到AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,再根据图形可得MN=MP+PN,即可得到答案.
解答 解:(1)∵M、N分别是AP、BP中点,
∴AM=PM=$\frac{1}{2}$AP=3,PN=$\frac{1}{2}$PB=2,
∴MN=MP+PN=3+2=5,
AB=AP+BP=6+4=10.
故答案为:10,5;
(2)∵AB=16,AP=10,
∴PB=AB-AP=16-10=6,
∵M、N分别是AP、BP中点,
∴AM=PM=$\frac{1}{2}$AP=5,PN=$\frac{1}{2}$PB=3,
∴MN=MP+PN=5+3=8.
故答案为:8.
(3)∵M、N分别是AP、BP中点,
∴AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,
∴MN=MP+PN=$\frac{1}{2}AP+\frac{1}{2}PB$=$\frac{1}{2}(AP+PB)$=$\frac{1}{2}AB$=$\frac{1}{2}×18$=9.
故答案为:9;
(4)∵M、N分别是AP、BP中点,
∴AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,
∴MN=MP+PN=$\frac{1}{2}AP+\frac{1}{2}PB$=$\frac{1}{2}(AP+PB)$=$\frac{1}{2}AB$=$\frac{1}{2}a$.
故答案为:$\frac{1}{2}a$.
点评 此题主要考查了求两点间的距离,解题的关键是根据条件理清线段之间的关系.

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
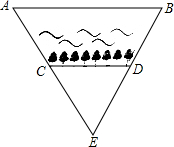 某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.
某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.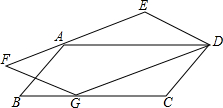 如图,ABCD是一个平行四边形,其面积等于8平方厘米,另一个平行四边形DEFG,EF过A点,G在BC上.问:平行四边形DEFG的面积是多少平方厘米?
如图,ABCD是一个平行四边形,其面积等于8平方厘米,另一个平行四边形DEFG,EF过A点,G在BC上.问:平行四边形DEFG的面积是多少平方厘米?