题目内容
4.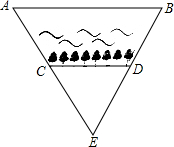 某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.
某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.(1)求护城河的宽度;
(2)若CE=24米,求AE的长度.
分析 (1)作EF⊥CD于F交AB于H,如图,EF=18m,CD=21m,AB=35m,证明△ECD∽△EAB,然后利用相似比计算HF即可;
(2)由于△ECD∽△EAB,则利用相似比可计算出AE的长.
解答 解:(1)作EF⊥CD于F交AB于H,如图,EF=18m,CD=21m,AB=35m,
∵CD∥AB,
∴△ECD∽△EAB,
∴$\frac{CD}{AB}$=$\frac{EF}{EH}$,即$\frac{21}{35}$=$\frac{18}{18+HF}$,
解得HF=12.
答:护城河的宽度为12m;
(2)∵△ECD∽△EAB,
∴$\frac{EC}{EA}$=$\frac{CD}{AB}$,即$\frac{24}{EA}$=$\frac{21}{35}$,
解得EA=40.
答:AE的长度为40m.
点评 本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | 3-2=-9 | B. | 3-2=9 | C. | 3-2=$\frac{1}{9}$ | D. | 3-2=-$\frac{1}{9}$ |
 如图,方格纸中的每个小正方形的边长均为1,点A,B在小正方形的顶点上,画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(至少两边长为无理数).
如图,方格纸中的每个小正方形的边长均为1,点A,B在小正方形的顶点上,画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(至少两边长为无理数). 东方明珠电视塔高468m,如果把塔身看作一条线段AC,中间的球体看作点B,那么点B是线段AC的黄金分割线,求AB的长(精确到0.1m)
东方明珠电视塔高468m,如果把塔身看作一条线段AC,中间的球体看作点B,那么点B是线段AC的黄金分割线,求AB的长(精确到0.1m) 如图,有一圆台形工件,要测量锥角的大小(即∠COD),工人师傅采用图中的办法,测量出∠AOB的大小,就是∠COD的大小,为什么,请说明理由.
如图,有一圆台形工件,要测量锥角的大小(即∠COD),工人师傅采用图中的办法,测量出∠AOB的大小,就是∠COD的大小,为什么,请说明理由.