题目内容
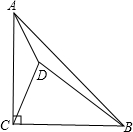 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是△ABC内一点,AD=2,DC、DB的长是关于x的方程x2-kx+24=0的两个实数根x1、x2,且x12+x22-x1x2=28.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是△ABC内一点,AD=2,DC、DB的长是关于x的方程x2-kx+24=0的两个实数根x1、x2,且x12+x22-x1x2=28.(1)画出△ACD绕点C顺时针旋转90°后所得的△BCE;
(2)求DC、BD和ED的长,并判断△BDE的形状;
(3)求∠ADC的度数和AC的长.
考点:作图-旋转变换,根与系数的关系
专题:
分析:(1)作CE⊥CD,取CE=CD,然后连接BE、DE即可得解;
(2)由根与系数的关系得,x1+x2=k,x1x2=24,然后代入等式求出k的值,再求出x1、x2,即为DC、BD的长,根据旋转的性质可得CE=CD,BE=AD,然后判断出△CDE是等腰直角三角形,根据等腰直角三角形的性质求出DE即可;再利用勾股定理逆定理判断△BDE是直角三角形;
(3)求出∠CEB,再根据全等三角形对应角相等可得∠ADC=∠CEB;求出AE,然后根据S△ABC=S△CDE+S△ABE列出方程求解即可.
(2)由根与系数的关系得,x1+x2=k,x1x2=24,然后代入等式求出k的值,再求出x1、x2,即为DC、BD的长,根据旋转的性质可得CE=CD,BE=AD,然后判断出△CDE是等腰直角三角形,根据等腰直角三角形的性质求出DE即可;再利用勾股定理逆定理判断△BDE是直角三角形;
(3)求出∠CEB,再根据全等三角形对应角相等可得∠ADC=∠CEB;求出AE,然后根据S△ABC=S△CDE+S△ABE列出方程求解即可.
解答: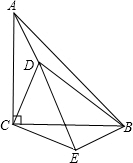 解:(1)如图所示;
解:(1)如图所示;
(2)由根与系数的关系得,x1+x2=k,x1x2=24,
∵x12+x22-x1x2=(x1+x2)2-3x1x2,
∴k2-3×24=28,
解得k1=10,k2=-10(舍去),
所以,原方程为x2-10x+24=0,
解得x1=4,x2=6,
所以,DC=4,DB=6,
由旋转的性质得,CE=CD=4,BE=AD=2,
所以,△CDE是等腰直角三角形,
所以,DE=
CD=4
,
∵DE2+BE2=(4
)2+22=36,
BD2=62=36,
∴DE2+BE2=BD2,
∴△BDE是直角三角形;
(3)∵△CDE是等腰直角三角形,△BDE是直角三角形,
∴∠CED=45°,∠BED=90°,
∴∠CEB=45°+90°=135°,
∵△ACD绕点C顺时针旋转90°后所得的△BCE,
∴∠ADC=∠CEB=135°;
∵∠ADC+∠CDE=135°+45°=180°,
∴点A、D、E三点共线,
∴AE=AD+DE=2+4
,
由旋转的性质得△ACD≌△BCE,
所以,S△ABC=S△CDE+S△ABE,
所以,
AC2=
AE•BE+
CD2,
即
AC2=
×(2+4
)×2+
×42,
解得AC=
.
 解:(1)如图所示;
解:(1)如图所示;(2)由根与系数的关系得,x1+x2=k,x1x2=24,
∵x12+x22-x1x2=(x1+x2)2-3x1x2,
∴k2-3×24=28,
解得k1=10,k2=-10(舍去),
所以,原方程为x2-10x+24=0,
解得x1=4,x2=6,
所以,DC=4,DB=6,
由旋转的性质得,CE=CD=4,BE=AD=2,
所以,△CDE是等腰直角三角形,
所以,DE=
| 2 |
| 2 |
∵DE2+BE2=(4
| 2 |
BD2=62=36,
∴DE2+BE2=BD2,
∴△BDE是直角三角形;
(3)∵△CDE是等腰直角三角形,△BDE是直角三角形,
∴∠CED=45°,∠BED=90°,
∴∠CEB=45°+90°=135°,
∵△ACD绕点C顺时针旋转90°后所得的△BCE,
∴∠ADC=∠CEB=135°;
∵∠ADC+∠CDE=135°+45°=180°,
∴点A、D、E三点共线,
∴AE=AD+DE=2+4
| 2 |
由旋转的性质得△ACD≌△BCE,
所以,S△ABC=S△CDE+S△ABE,
所以,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
解得AC=
10+4
|
点评:本题考查了利用旋转变换作图,根与系数的关系,等腰直角三角形的判定与性质,勾股定理逆定理,难点在于(3)判断出点A、D、E三点共线并利用三角形的面积列出方程.

练习册系列答案
相关题目