题目内容
16.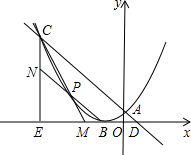 如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.(1)则∠CDE=45°;
(2)求抛物线对应的函数关系式;
(3)设P(x,y)为抛物线上一点(其中-3<x<-1或-1<x<1,
连结BP并延长交直线CE于点N,记N点的纵坐标为yN,连结CP并延长交X轴于点M.
①试证明:EM•(EC+yN)为定值;
②试判断EM+EC+yN是否有最小值,并说明理由.
分析 (1)根据AE=m-3-(-3)=m,CE=m,得到AE=CE,从而得到∠EAC=45°;
(2)设E点横坐标为xE,D点横坐标为xD,则ED=xD-xE=m,又C(-3,m),可知,A(0,m-3),C(-3,m),设抛物线的方程为y=a(x+1)2,代入求值即可;
(3))①设P(x,x2+2x+1),作PQ⊥x轴于Q,根据EM•(EC+yN)=$\frac{4}{1-x}$•(-2x-2+4)=8可知为定值;
②求出y=s+t=t+$\frac{8}{t}$=($\sqrt{t}$-$\frac{2\sqrt{2}}{\sqrt{t}}$)2+4$\sqrt{2}$,求出最小值.
解答 解:(1)∵AE=m-3-(-3)=m,CE=m,
∴AE=CE,
∴∠EAC=45°.
(2)设E点横坐标为xE,D点横坐标为xD,
则ED=xD-xE=m,又C(-3,m),
∴EC=ED,即∠CDE=45°,
∴OA=OD=m-3,即A(0,m-3),
设抛物线的方程为y=a(x+1)2,则$\left\{\begin{array}{l}m=4a\\ m-3=a\end{array}\right.$,
解得,a=1,m=4,故抛物线方程为y=(x+1)2.
(3)①设P(x,x2+2x+1),作PQ⊥x轴于Q,如图: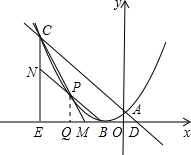
由Rt△BPQ∽Rt△BNE,可得yN=-2(x+1),
由Rt△MPQ∽Rt△MCE可得,EM=$\frac{4}{1-x}$,
∴EM•(EC+yN)=$\frac{4}{1-x}$•(-2x-2+4)=8(为定值)(-3<x<-1和-1<x<1两种情况完全相同).
②有最小值.
记y=EM+EC+yN,s=EM,t=EC+yN,由①st=8,
∴y=s+t=t+$\frac{8}{t}$=($\sqrt{t}$-$\frac{2\sqrt{2}}{\sqrt{t}}$)2+4$\sqrt{2}$,
此时,($\sqrt{t}$-$\frac{2\sqrt{2}}{\sqrt{t}}$)2=0,化简得t=2$\sqrt{2}$,即x=1-$\sqrt{2}$时,取到最小值.
点评 本题考查了二次函数综合题,涉及坐标与图形的关系、等腰直角三角形的判定、二次函数的最值等,综合性强,值得关注.

| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
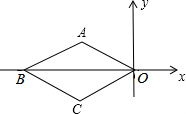 如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$). 一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).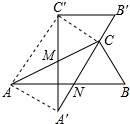 有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
 如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′. 如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.
如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.