题目内容
8．
如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB为x米，面积为y平方米．（1）求y与x之间的函数关系式；
（2）当x取何值时所围成的花圃的面积最大？最大面积是多少？
分析 （1）根据花圃的宽AB为x米，得出BC，再根据长方形的面积公式列式计算即可；
（2）根据y与x之间的函数关系式求出函数的最值即可．
解答 解：（1）∵花圃的宽AB为x米，
∴BC=（24-4x）米，
∴y=x（24-4x）=-4x2+24x；
（2）∵y=-4x2+24x=-4（x-3）2+36，
∴当x=3时，y最大值=36，
答；当x取3时所围成的花圃的面积最大，最大面积是36平方米．
点评 本题主要考查了二次函数的应用，用到的知识点是二次函数的最值、二次函数的解析式、长方形的面积，能把实际问题转化成数学问题是解此题的关键．
练习册系列答案
相关题目
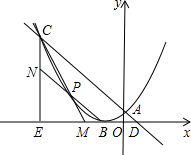如图所示，已知点C（-3，m），点D（m-3，0）．直线CD交y轴于点A．作CE与X轴垂直，垂足为E，以点B（-1，0）为顶点的抛物线恰好经过点A、C．
按要求作图，并标出位置．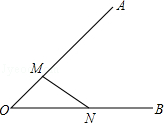
如图，在图中求作一⊙P，使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等，保留作图痕迹不写出作法．（要求：用尺规作图）
如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（ ）
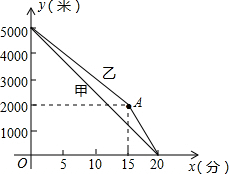甲乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数的图象如图所示，根据图象所提供的信息解答下列问题：