题目内容
4. 一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).
分析 根据三视图得到几何体为圆锥,圆锥的高为$\sqrt{3}$,圆锥底面圆的半径为1,则根据勾股定理可计算出母线长,然后计算侧面积和底面积的和即可.
解答 解:由三视图得几何体为圆锥,圆锥的高为$\sqrt{3}$,圆锥底面圆的半径为1,
所以圆锥的母线长=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,
所以圆锥的表面积=π•12+$\frac{1}{2}$•2π•1•2=3π.
故答案为3π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
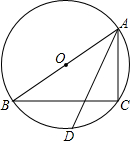 如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.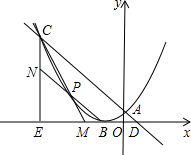 如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C. 如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,
如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时, 按要求作图,并标出位置.
按要求作图,并标出位置.