题目内容
11.设函数y=x+5与$y=\frac{3}{x}$的图象的两个交点的横坐标为a、b,则$\frac{1}{a}+\frac{1}{b}$的值是( )| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
分析 联立两函数解析式,消掉y,得到关于x的一元二次方程,然后利用根与系数的关系求解即可.解关于x、y的二元一次方程组求出a、b的值,然后代入进行计算即可得解.
解答 解:联立$\left\{\begin{array}{l}{y=x+5}\\{y=\frac{3}{x}}\end{array}\right.$消掉y得,x2+5x-3=0,
∵两个交点的横坐标为a、b,
∴a+b=-5,ab=-3,
∴$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{-5}{-3}$=$\frac{5}{3}$.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题,联立两函数解析式得到关于x的一元二次方程是解题的关键,利用根与系数的关系式求解要不求出a、b的值更加简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
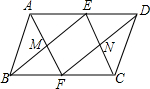 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )
已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )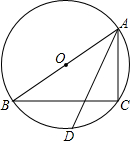 如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.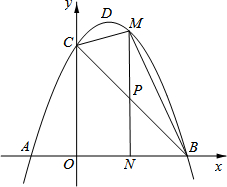 如图,抛物线y=-x2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.
如图,抛物线y=-x2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.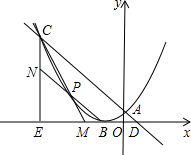 如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.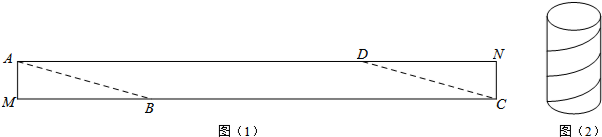
 在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.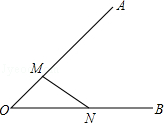 如图,在图中求作一⊙P,使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等,保留作图痕迹不写出作法.(要求:用尺规作图)
如图,在图中求作一⊙P,使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等,保留作图痕迹不写出作法.(要求:用尺规作图)