题目内容
6.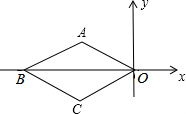 如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
分析 首先由题意可得点M第39次移动到点C,然后过点C作CD⊥x轴于点D,由四边形OAC是菱形,可求得∠COD=30°,OC=OA=$\sqrt{3}$,再利用含30°角的直角三角形的性质,1求得CD的长,利用勾股定理求得OD的长,继而求得答案.
解答  解:∵点M四次一循环,
解:∵点M四次一循环,
∴39÷4=9…3,
∴点M第39次移动到点C,
过点C作CD⊥x轴于点D,
∵四边形OAC是菱形,
∴∠COD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×60°=30°,OC=OA=$\sqrt{3}$,
∴CD=$\frac{1}{2}$OC=$\frac{\sqrt{3}}{2}$,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=$\frac{3}{2}$,
∴点C的坐标为:(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$),
即点M第39次移动到的点的坐标是:(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
故答案为:(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 此题考查了菱形的性质以及含30°角的直角三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.-$\frac{1}{2}$的绝对值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
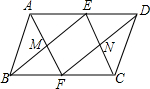 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )
已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( ) 如图:O是正方形ABCD对角线的交点,圆心角为90°的扇形EOF从图1位置,顺时针旋转到图2位置,OE、OF分别交AD、AB于G、H.
如图:O是正方形ABCD对角线的交点,圆心角为90°的扇形EOF从图1位置,顺时针旋转到图2位置,OE、OF分别交AD、AB于G、H.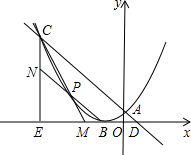 如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.