题目内容
7．
如图．E是?ABCD内任一点，若S?ABCD=6，则S△ABE+S△CDE=3．
分析 由S?ABCD=6，易得S△ABD=S△CBD=3，又由S△ABE=$\frac{BE}{BD}$S△ABD与S△CDE=$\frac{DE}{BD}$S△CBD求解的答案．
解答 解：∵四边形ABCD是平行四边形，
∴S△ABD=S△CBD=$\frac{1}{2}$S?ABCD=$\frac{1}{2}$×6=3，
∵S△ABE=$\frac{BE}{BD}$S△ABD=$\frac{3BE}{BD}$，S△CDE=$\frac{DE}{BD}$S△CBD=$\frac{3DE}{BD}$，
∴S△ABE+S△CDE=$\frac{3BE+3DE}{BD}$=$\frac{3BD}{BD}$=3．
故答案为：3．
点评 此题考查了平行四边形的性质以及三角形的面积问题．注意等高三角形面积的比等于对应底的比．
练习册系列答案
相关题目
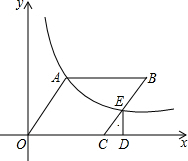如图，在平面直角坐标系中，?OABC的顶点C的坐标为（3，0），∠AOC=45°，反比例函数y=$\frac{k}{x}$（k＞0）的图象经过点A交BC于点E，过点E作ED⊥x轴于点D，ED=1．
如图，AB=AC，D、E分别是AB、AC的中点，AM⊥CD于M，AN⊥BE干N．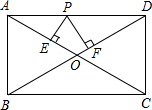
如图，在矩形ABCD中，P是边AD上的动点，PE⊥AC于点E，PF⊥BD于点F．如果AB=5，AD=9．那么PE+PF的值．
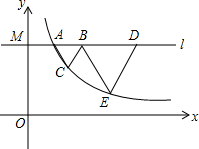如图，过点M（0，3）的直线l平行于x轴，交反比例函数y=$\frac{k}{x}$的图象于点A，B、D是直线l上的点且满足$\frac{AB}{BD}$=$\frac{1}{2}$，以AB，BD为边向下作等边△ABC和等边△BDE，当C，E都落在y=$\frac{k}{x}$的图象上时，k=$\frac{6\sqrt{3}}{7}$．
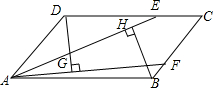如图，在平行四边形ABCD中，点E，F分别在BC，CD上，且AE=AF，DG⊥AE，BH⊥AF，点G，H为垂足，猜想DG与BH的大小关系，并证明你的猜想．
如图，在?ABCD中，BD⊥AD，AD=8，AB=10，则AC的长为2$\sqrt{73}$．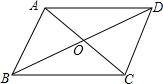
平行四边形ABCD的两条对角线AC，BD相交于点O．