题目内容
6.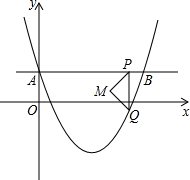 如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.(1)求这条抛物线所对应的函数表达式.
(2)当线段PQ被x轴平分时,求m的值.
(3)当等腰直角三角形PQM夹在x轴与直线AB之间的图形为轴对称三角形时,求m的取值范围.
(4)直接写出当等腰直角三角形PQM的两条直角边与坐标轴有两个公共点时m的取值范围.
分析 (1)将A点坐标代入解析式直接求出a;
(2)由P、Q关于x轴对称,且横坐标相同可设出Q点坐标,代入抛物线解析式中,即可直接求出m的值;
(3)找到两个临界点:当Q点刚好在x轴上时;当M点刚好在x轴上时.算出这个两个临界状态时的m值,即可确定符合要求的m的取值范围;
(4)等腰直角三角形PQM的两条直角边与坐标轴有两个公共点,也就是y轴同时与两直角边相交,所以只需算出M点恰好在y轴上的临界状态时的m值即可.
解答 解:(1)把A(0,1)代入y=a(x-2)2-2中,得1=a(0-2)2-2,
∴a=$\frac{3}{4}$,
∴y=$\frac{3}{4}$(x-2)2-2,
(2)设Q(m,-1),
则-1=$\frac{3}{4}$(m-2)2-2,
∴m1=2+$\frac{2}{3}\sqrt{3}$,m2=2-$\frac{2}{3}\sqrt{3}$.
(3)当点Q落在x轴上时,PQ=1,
∴1-[$\frac{3}{4}$(m-2)2-2]=1,
∴m1=2-$\frac{2}{3}\sqrt{6}$,m2=2+$\frac{2}{3}\sqrt{6}$,
∴当0<m≤2-$\frac{2}{3}\sqrt{6}$或2-$\frac{2}{3}\sqrt{3}$≤m≤2+$\frac{2}{3}\sqrt{3}$或2+$\frac{2}{3}\sqrt{6}$≤m<4,为轴对称三角形,
(4)当M点刚好在y轴上时:$\frac{1}{2}$|1-[$\frac{3}{4}$(m-2)2-2]|=m,
解得:m=$\frac{4}{3}$或m=$\frac{20}{3}$,
由图象可知,当等腰直角三角形PQM的两条直角边与坐标轴有两个公共点时m的取值范围
∴2-$\frac{2}{3}$$\sqrt{6}$<m<$\frac{4}{3}$或m>$\frac{20}{3}$.
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数解析式、等腰直角三角形的性质、线段长度的坐标表示、解一元二次方程、轴对称图形等知识点,难度中等.本题巧妙地将动态几何与二次函数结合,具有较强的综合性,对学生的分析能力、想象力提出了较高要求.解答过程中,找准临界状态并正确列出方程是关键.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案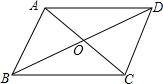 平行四边形ABCD的两条对角线AC,BD相交于点O.
平行四边形ABCD的两条对角线AC,BD相交于点O.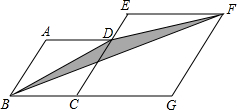 如图,菱形ABCD与菱形ECGF中,点D在CE上,点B、C、G在一条直线上,AB=2,CG=4,∠ABC=60°,连接BD,DF,BF,则图中阴影部分的周长为$\sqrt{3}$.
如图,菱形ABCD与菱形ECGF中,点D在CE上,点B、C、G在一条直线上,AB=2,CG=4,∠ABC=60°,连接BD,DF,BF,则图中阴影部分的周长为$\sqrt{3}$.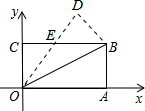 如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,试求点D的坐标.
如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,试求点D的坐标. 在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE,垂足为F.求证:AE=AD.
在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE,垂足为F.求证:AE=AD.