题目内容
19.有五张正面分别标有数-2,0,1,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将卡片上的数记为a,则使关于x的方程$\frac{1-ax}{x-1}$-3=$\frac{3x}{1-x}$有正整数解的概率为$\frac{1}{5}$.分析 易得分式方程的解,看所给5个数中,能使分式方程有整数解的情况数占总情况数的多少即可.
解答 解:解分式方程得:x=$\frac{4}{a}$,
∵分式方程的解为正整数,
∴a>0,
又∵x≠1,
∴a≠4,
∴a=1,
∴使关于x的分式方程有正整数解的概率为$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查概率的基本计算,用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
相关题目
9.某酒店客房有三人间、双人间客房,收费标准如下:
为吸引游客,实行团体入住五折优惠.一个40人的旅游团在优惠期间到该酒店入住,住了一些三人间普通和双人间普通客房.若每间客房正好住满,且一天共花去住宿费1220元,则旅游团住了三人间普通和双人间普通客房各多少间?
| 普通(元/间/天) | 豪华(元/间/天) | |
| 三人间 | 150 | 300 |
| 双人间 | 140 | 400 |
7.下列计算正确的是( )
| A. | 2t-t=2 | B. | t2•t3=t6 | C. | (-t2)3=-t5 | D. | t3÷t2=t |
11.一元一次不等式组$\left\{\begin{array}{l}{2x-1<3}\\{x+3>2x}\end{array}\right.$的解是( )
| A. | -2<x<3 | B. | -3<x<2 | C. | x<-3 | D. | x<2 |
8.-$\frac{1}{3}$的绝对值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 0 |
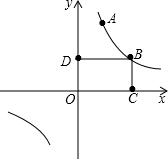 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.