题目内容
14.图1是某希望小学放心食堂售饭窗口外遮雨棚的示意图(尺寸如图所示),遮雨棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是遮雨棚顶部截面的示意图,$\widehat{AB}$所在圆的圆心为O.遮雨棚顶部是用一种帆布覆盖的,求覆盖遮雨棚顶的帆布的面积(不考虑接缝等因素,计算结果保留π ).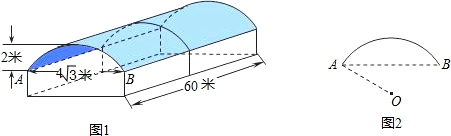
分析 根据题意,由圆的基本性质,可通过作辅助线建立模形,将车棚顶部展开得长方形,利用垂径定理解答.
解答 解:连接OB,过点O作OE⊥AB,垂足为E,交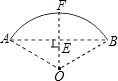 $\widehat{AB}$于F,如图,
$\widehat{AB}$于F,如图,
由垂径定理,可知:E是AB中点,F是$\widehat{AB}$中点,
∴EF是弓形高,
∴AE=$\frac{1}{2}$AB=2$\sqrt{3}$,EF=2,
设半径为R米,则OE=(R-2)米,
在Rt△AOE中,由勾股定理,得R2=(R-2)2+(2$\sqrt{3}$)2,
解得R=4,
∵sin∠AOE=$\frac{AE}{OA}$,
∴∠AOE=60°,
∴∠AOB=120度.
∴$\widehat{AB}$的长为$\frac{120×4π}{180}$=$\frac{8}{3}$π(m),
∴帆布的面积为$\frac{8}{3}$π×60=160π(平方米).
点评 本题考查了垂径定理和勾股定理的应用,解答本题的关键是把实际问题与数学中的理论知识联系起来,将车棚顶部展开得长方形,然后求其面积.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.某酒店客房有三人间、双人间客房,收费标准如下:
为吸引游客,实行团体入住五折优惠.一个40人的旅游团在优惠期间到该酒店入住,住了一些三人间普通和双人间普通客房.若每间客房正好住满,且一天共花去住宿费1220元,则旅游团住了三人间普通和双人间普通客房各多少间?
| 普通(元/间/天) | 豪华(元/间/天) | |
| 三人间 | 150 | 300 |
| 双人间 | 140 | 400 |
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
 如图,在△ABC中,D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S△ADE的值.
如图,在△ABC中,D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S△ADE的值.




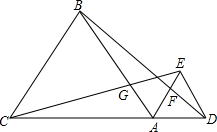 如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.
如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.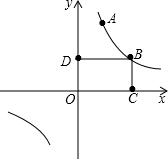 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.