题目内容
5.解不等式组$\left\{\begin{array}{l}{\frac{x-3}{4}+6≥x①}\\{4-5(x-2)<4(2-x)②}\end{array}\right.$,并判断x=3$\sqrt{5}$是不是这个不等式组的解.分析 先解不等式①,再解不等式②,取不等式①②的解集的公共部分即可得出不等式组的解集,再判断即可.
解答 解:解不等式①,得x≤7;
解不等式②,得x>6;
不等式组的解集为6<x≤7;
∵6<3$\sqrt{5}$≤7,
∴x=3$\sqrt{5}$是这个不等式组的解.
点评 本题考查了解一元一次不等式组以及把不等式组的解集画在数轴上,掌握不等式的解法是解题的关键.

练习册系列答案
相关题目
15.已知a+b+c=0,则$\frac{\sqrt{{a}^{2}}}{a}+\frac{\sqrt{{b}^{2}}}{b}+\frac{\sqrt{{c}^{2}}}{c}$的值可能是1或-1.
7.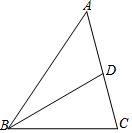 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |

 在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=30°;∠E=60°.
在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=30°;∠E=60°.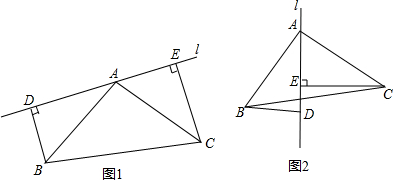
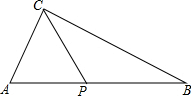 如图,Rt△ABC中,∠C=90°,AC=2,BC=4,P是AB边上的一个动点.
如图,Rt△ABC中,∠C=90°,AC=2,BC=4,P是AB边上的一个动点.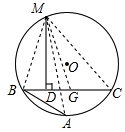 请阅读下列材料,并完成相应的任务:
请阅读下列材料,并完成相应的任务: