题目内容
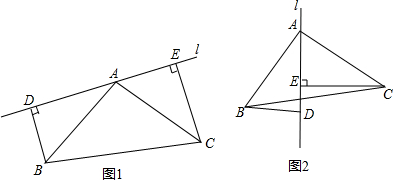
3.如图,在△ABC中,AB=AC,l是过点A的直线,BD⊥直线l于点D,CE⊥直线l于点E(1)若点B,C在直线l的同侧(如图1所示),且AD=CE.求证:AB⊥AC;
(2)若点B,C在直线l的两侧(如图2所示),其他条件不变,(1)中结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
分析 (1)只要证明△ABD≌△ACE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC;
(2)结论仍然成立,证明方法类似.
解答 (1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=CE}\end{array}\right.$,
∴Rt△ABD≌Rt△CAE(HL).
∴∠DAB=∠ECA,
∵∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∴∠BAC=180°-(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)解:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=CE}\end{array}\right.$,
∴Rt△ABD≌Rt△CAE(HL).
∴∠DAB=∠ECA,
∵∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∴∠BAC=180°-(∠BAD+∠CAE)=90°.
∴AB⊥AC.
点评 本题考查了全等三角形的判定与性质、直角三角形的性质和判定等知识,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.抛物线y=2(x+3)2-2的顶点坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |

 (1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)
(1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)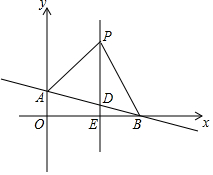 如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).