题目内容
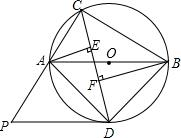 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.考点:切线的性质
专题:探究型
分析:根据圆周角定理得∠ACB=90°,利用角平分线的定义得∠ACD=∠BCD=45°,由于AE⊥CD,则可判断△ACE等腰直角三角形,得到AE=CE,同理得CF=FB,于是FB=CF=CE+EF=AE+EF.
解答:证明:FB=AE+EF.理由如下:
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
又∵AE⊥CD,
∴△ACE等腰直角三角形,
∴AE=CE,
∵∠ACB的平分线交⊙O于点D,
∴∠DAB=45°,
又∵BF⊥CD,
∴△CFB为等腰直角三角形,
∴CF=FB,
∴FB=CF=CE+EF=AE+EF.
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
又∵AE⊥CD,
∴△ACE等腰直角三角形,
∴AE=CE,
∵∠ACB的平分线交⊙O于点D,
∴∠DAB=45°,
又∵BF⊥CD,
∴△CFB为等腰直角三角形,
∴CF=FB,
∴FB=CF=CE+EF=AE+EF.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和等腰直角三角形的判定与性质.

练习册系列答案
相关题目
 如图,它们是一个物体的三视图,该物体的形状是( )
如图,它们是一个物体的三视图,该物体的形状是( )A、 |
B、 |
C、 |
D、 |
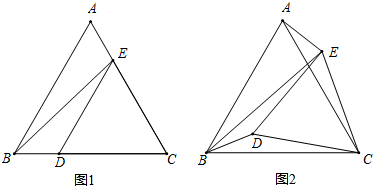 已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.
已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.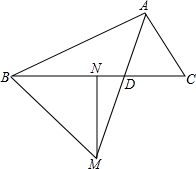 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.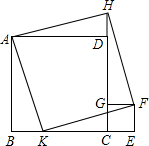 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形. 画出如图立体图形的三视图.
画出如图立体图形的三视图.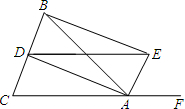 如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE. 有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=
有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=