题目内容
某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40~65元之间.市场调查发现:若每箱以50元销售,平均每天可销售90箱;价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱.
(1)写出平均每天销售y(箱)与每箱售价x(元)之间的关系式;
(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的关系式(每箱的利润=售价-进价);
(3)当每箱牛奶售价为多少时,平均每天的利润最多.
(1)写出平均每天销售y(箱)与每箱售价x(元)之间的关系式;
(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的关系式(每箱的利润=售价-进价);
(3)当每箱牛奶售价为多少时,平均每天的利润最多.
考点:二次函数的应用
专题:
分析:(1)根据销售数量与售价的关系分类讨论,当x>50或x<50时分别求出y与x之间的函数关系式;
(2)由销售问题的数量关系根据销售数量×每箱的利润就可以求出总利润;
(3)由(2)的解析式化为顶点式即可求出结论.
(2)由销售问题的数量关系根据销售数量×每箱的利润就可以求出总利润;
(3)由(2)的解析式化为顶点式即可求出结论.
解答:解:(1)由题意,得
当x>50时,
y=90-3(x-50)=240-3x
当x<50时,
y=90+3(50-x)=240-3x;
(2)由题意,得
W=(240-3x)(x-40)=-3x2+360x-9600.
∴W=-3x2+360x-9600.
答:利润W(元)与每箱牛奶的售价x(元)之间的关系式为W=-3x2+360x-9600;
(3)∵W=-3x2+360x-9600,
∴W=-3(x-60)2+1200.
∴a=-3<0,抛物线开口向下,W有最大值,
∴x=60时,W最大=1200.
答:每箱牛奶售价为60元时,平均每天的利润最多为1200元.
当x>50时,
y=90-3(x-50)=240-3x
当x<50时,
y=90+3(50-x)=240-3x;
(2)由题意,得
W=(240-3x)(x-40)=-3x2+360x-9600.
∴W=-3x2+360x-9600.
答:利润W(元)与每箱牛奶的售价x(元)之间的关系式为W=-3x2+360x-9600;
(3)∵W=-3x2+360x-9600,
∴W=-3(x-60)2+1200.
∴a=-3<0,抛物线开口向下,W有最大值,
∴x=60时,W最大=1200.
答:每箱牛奶售价为60元时,平均每天的利润最多为1200元.
点评:本题考查了销售问题的数量关系每箱的利润=售价-进价的运用,二次函数的解析式的运用,二次函数的性质的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
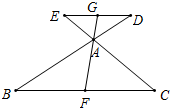 如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.
如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.
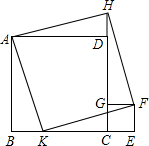 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形. 用一段长为30米的篱笆围成一个一边靠墙(墙长为12米)的矩形菜园ABCD,设AB长为x米,菜园的面积为y平方米.
用一段长为30米的篱笆围成一个一边靠墙(墙长为12米)的矩形菜园ABCD,设AB长为x米,菜园的面积为y平方米.  如图,在△ABC中,AM平分∠A,BD⊥AM,交AM延长线于点D,DE∥CA交AB于E,求证:AE=BE.
如图,在△ABC中,AM平分∠A,BD⊥AM,交AM延长线于点D,DE∥CA交AB于E,求证:AE=BE. 如图所示,已知AD∥EF∥BC,FG∥CH.求证:
如图所示,已知AD∥EF∥BC,FG∥CH.求证: 如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.
如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.