题目内容
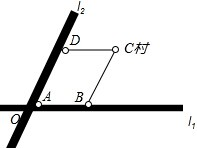 如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是
如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是考点:全等三角形的应用,角平分线的性质
专题:
分析:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,先根据SSS证明△ADC≌△ABC,得出∠DAC=∠BAC,即AC平分∠BAD,然后根据角平分线的性质,即可求得答案.
解答: 解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,
解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,
在△ADC与△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
∵CE⊥l2于E,CF⊥l1于F,
∴CE=CF=4km,
即村庄C到公路l2的距离是4km.
故答案是:4.
 解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,
解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,在△ADC与△ABC中,
|
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
∵CE⊥l2于E,CF⊥l1于F,
∴CE=CF=4km,
即村庄C到公路l2的距离是4km.
故答案是:4.
点评:此题考查了全等三角形的应用以及角平分线的性质.此题难度不大,注意掌握辅助线的作法,证明△ADC≌△ABC,得出∠DAC=∠BAC是解题的关键.

练习册系列答案
相关题目
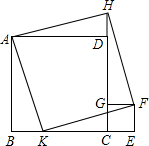 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形. 有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=
有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|= 如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.
如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.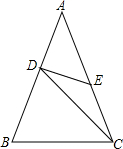 如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)
如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)