题目内容
 如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.
如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:过点A作CN的垂线,垂足为B,连接BM、CM,求出∠ACB=∠CON,根据AAS推出△ABC≌△CNO,根据全等三角形的性质得出AB=CN,根据等腰直角三角形的性质得出∠AMC=90°,AM=CM,求出∠BAM=∠NCM,根据SAS推出△BAM≌△NCM,求出MB=MN,∠AMB=∠CMN,求出∠BMN=∠AMC=90°,推出△BMN是等腰直角三角形,求出∠BNM=45°即可.
解答:解:
过点A作CN的垂线,垂足为B,连接BM、CM,
∵∠ACB+∠OCN=180°-90°=90°,∠OCN+∠CON=90°,
∴∠ACB=∠CON,
在△ABC和△CNO中
∴△ABC≌△CNO,
∴AB=CN,
∵△ACO是等腰直角三角形,M是AO的中点,
∴∠AMC=90°,AM=CM,
∴∠BAM+∠BCM=360°-∠ABC-∠AMC=180°,
∴∠BAM=∠NCM,
在△BAM和△NCM中
∴△BAM≌△NCM,
∴MB=MN,∠AMB=∠CMN,
∴∠BMN=∠BMC+∠CMN=∠BMC+∠AMB=∠AMC=90°,
∴△BMN是等腰直角三角形,
∴∠BNM=45°,
∴∠MNO=45°.

过点A作CN的垂线,垂足为B,连接BM、CM,
∵∠ACB+∠OCN=180°-90°=90°,∠OCN+∠CON=90°,
∴∠ACB=∠CON,
在△ABC和△CNO中
|
∴△ABC≌△CNO,
∴AB=CN,
∵△ACO是等腰直角三角形,M是AO的中点,
∴∠AMC=90°,AM=CM,
∴∠BAM+∠BCM=360°-∠ABC-∠AMC=180°,
∴∠BAM=∠NCM,
在△BAM和△NCM中
|
∴△BAM≌△NCM,
∴MB=MN,∠AMB=∠CMN,
∴∠BMN=∠BMC+∠CMN=∠BMC+∠AMB=∠AMC=90°,
∴△BMN是等腰直角三角形,
∴∠BNM=45°,
∴∠MNO=45°.
点评:本题考查了等腰直角三角形的性质和判定,全等三角形的性质和判定,直角三角形的性质的应用,解此题的关键是推出三角形BMN是等腰直角三角形,题目比较好,难度偏大.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
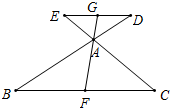 如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.
如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.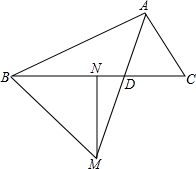 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
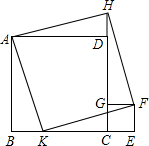 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形. 如图,在△ABC中,AM平分∠A,BD⊥AM,交AM延长线于点D,DE∥CA交AB于E,求证:AE=BE.
如图,在△ABC中,AM平分∠A,BD⊥AM,交AM延长线于点D,DE∥CA交AB于E,求证:AE=BE.