题目内容
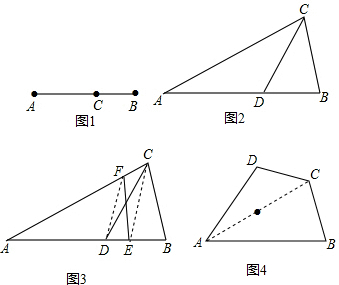
如图1,我们知道,若点C将切断AB分成两部分,且
=
,则称点C为线段AB的黄金分割点.类似地,我们可以给出“黄金分割点”的定义:若直线l将一个面积为S的图形分成两部分S1,S2,且
=
,则称直线l为该图形的黄金分割线.
(1)如图2,在△ABC中,若点D为AB边上的黄金分割点(靠近B),则直线CD是△ABC的黄金分割线吗?为什么?
(2)如图3,在△ABC中,D为AB的黄金分割点(靠近B),过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,则直线EF也为△ABC的黄金分割线,请你说明理由.
(3)如图4,四边形ABCD中,点E为AC的一个黄金分割点(靠近A),请你画出四边形ABCD的一条黄金分割线,简单写出画法步骤,并说明理由.
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |
(1)如图2,在△ABC中,若点D为AB边上的黄金分割点(靠近B),则直线CD是△ABC的黄金分割线吗?为什么?
(2)如图3,在△ABC中,D为AB的黄金分割点(靠近B),过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,则直线EF也为△ABC的黄金分割线,请你说明理由.
(3)如图4,四边形ABCD中,点E为AC的一个黄金分割点(靠近A),请你画出四边形ABCD的一条黄金分割线,简单写出画法步骤,并说明理由.

考点:黄金分割
专题:常规题型
分析:(1)根据三角形面积公式得到S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,再根据黄金分割的定义得到AD:AB=BD:AD,所以S△ACD:S△ABC=S△BCD:S△ACD,于是根据图形的黄金分割线定义即可得到CD是△ABC的黄金分割线;
(2)根据三角形面积公式,由DE∥CE得到S△DCF=S△EDF,则S△ACD=S△AEF,S△BCD=S四边形BCFE,利用S△ACD:S△ABC=S△BCD:S△ACD得到S△AEF:S△ABC=S四边形BCFE:S△AEF,所以可判断直线EF为△ABC的黄金分割线;
(3)连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.利用(2)的结论进行说明.
(2)根据三角形面积公式,由DE∥CE得到S△DCF=S△EDF,则S△ACD=S△AEF,S△BCD=S四边形BCFE,利用S△ACD:S△ABC=S△BCD:S△ACD得到S△AEF:S△ABC=S四边形BCFE:S△AEF,所以可判断直线EF为△ABC的黄金分割线;
(3)连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.利用(2)的结论进行说明.
解答:解:(1)∵S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
又∵D是AB的黄金分割点,
∴AD:AB=BD:AD,
S△ACD:S△ABC=S△BCD:S△ACD,
∴CD是△ABC的黄金分割线;
(2)∵DE∥CE,
∴S△DCF=S△EDF,
∴S△ACD=S△AEF,
∴S△BCD=S四边形BCFE,
∵S△ACD:S△ABC=S△BCD:S△ACD,
∴S△AEF:S△ABC=S四边形BCFE:S△AEF,
∴直线EF为△ABC的黄金分割线;
(3) 连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.理由如下:
连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.理由如下:
∵点E为AC的一个黄金分割点(靠近A),
∴S△AED:S△DEC=S△DCE:S△ACD,S△ABE:S△EBC=S△BCE:S△ABC,
∵MN∥BD,
∴S△MEB=S△MED,
∴S四边形BCDM=S四边形BCDE=S△DCE+S△BCE,
S△ABM=S△ADE+S△ABE,
∴S△ABM:S四边形BCDM=S四边形BCDM:S四边形ABCD,
∴BM为四边形ABCD的一条黄金分割线.
又∵D是AB的黄金分割点,
∴AD:AB=BD:AD,
S△ACD:S△ABC=S△BCD:S△ACD,
∴CD是△ABC的黄金分割线;
(2)∵DE∥CE,
∴S△DCF=S△EDF,
∴S△ACD=S△AEF,
∴S△BCD=S四边形BCFE,
∵S△ACD:S△ABC=S△BCD:S△ACD,
∴S△AEF:S△ABC=S四边形BCFE:S△AEF,
∴直线EF为△ABC的黄金分割线;
(3)
 连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.理由如下:
连结BE、DE、BD,过点E作MN∥BD分别交AD、AB于M、N,连结BM,则BM为四边形ABCD的一条黄金分割线.理由如下:∵点E为AC的一个黄金分割点(靠近A),
∴S△AED:S△DEC=S△DCE:S△ACD,S△ABE:S△EBC=S△BCE:S△ABC,
∵MN∥BD,
∴S△MEB=S△MED,
∴S四边形BCDM=S四边形BCDE=S△DCE+S△BCE,
S△ABM=S△ADE+S△ABE,
∴S△ABM:S四边形BCDM=S四边形BCDM:S四边形ABCD,
∴BM为四边形ABCD的一条黄金分割线.
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从方程组
中求x与y的关系是( )
|
| A、x+y=-1 |
| B、x+y=1 |
| C、2x-y=7 |
| D、x+y=9 |
轮船航行到C处观测小岛A的方向是北偏西54°,那么从A同时观测轮船在C处的方向是( )
| A、南偏东54° |
| B、东偏北36° |
| C、东偏南54° |
| D、南偏东36° |
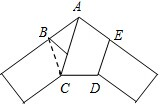 将固定宽度的纸条打一个简单的结,然后系紧,使它成为一个平面的结,如图所示,求证:这个五边形是正五边形.
将固定宽度的纸条打一个简单的结,然后系紧,使它成为一个平面的结,如图所示,求证:这个五边形是正五边形.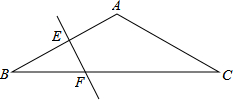 在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF=
在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF= 如图,点A和点B分别是棱长为20cm的正方体盒子上两条棱的中点,一只昆虫沿盒子的表面由A处爬行到B处,所走的最短路程是多少?
如图,点A和点B分别是棱长为20cm的正方体盒子上两条棱的中点,一只昆虫沿盒子的表面由A处爬行到B处,所走的最短路程是多少?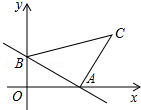 如图,一次函数y=-
如图,一次函数y=-