题目内容
11．已知两边的长分别为8和15，若要组成一个直角三角形，则第三边应该为17或$\sqrt{161}$．分析 根据勾股定理的内容，两直角边的平方和等于斜边的平方，分两种情况进行解答．
解答 解：分两种情况进行讨论：
①两直角边分别为8，15，由勾股定理得第三边应该为$\sqrt{{8}^{2}+1{5}^{2}}$=17，
②一直角边为8，一斜边为15，由勾股定理得第三边应该为$\sqrt{1{5}^{2}-{8}^{2}}$=$\sqrt{161}$，
故答案为17或$\sqrt{161}$．
点评 本题考查了利用勾股定理解直角三角形的能力，当已知条件中没有明确哪是斜边时，要注意讨论，一些学生往往忽略这一点，造成丢解．
练习册系列答案
相关题目
16．在△ABC中，三条边长分别为a，b，c，且a=n，b=$\frac{{n}^{2}}{4}$-1，c=$\frac{{n}^{2}}{4}$+1（n是大于2的偶数），求证：△ABC是直角三角形．
3．
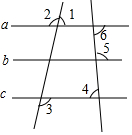如图，下列命题是假命题的是（ ）
如图，下列命题是假命题的是（ ）| A． | 如果∠2=∠3，那么a∥c | B． | 如果a∥b，a∥c，那么b∥c | ||
| C． | 如果∠4+∠5=180°，那么∠2=∠3 | D． | 如果∠4=∠6，那么∠1+∠3=180° |
20．若关于x的一元二次方程为ax2+bx+5=0（a≠0）的解是x=1，则2013-a-b的值是（ ）
| A． | 2 018 | B． | 2 008 | C． | 2 014 | D． | 2 012 |
