题目内容
16.在△ABC中,三条边长分别为a,b,c,且a=n,b=$\frac{{n}^{2}}{4}$-1,c=$\frac{{n}^{2}}{4}$+1(n是大于2的偶数),求证:△ABC是直角三角形.分析 判断一组数能否成为直角三角形的三边,就是看是否满足两较小边的平方和等于最大边的平方即可.
解答 证明:△ABC是直角三角形,
理由如下:
∵(n)2+($\frac{{n}^{2}}{4}$-1)2=($\frac{{n}^{2}}{4}$+1)2,
∴a2+b2=c2,
∴△ABC是直角三角形.
点评 本题考查了勾股定理的逆定理的应用,在应用时注意是两较短边的平方和等于最长边的平方.

练习册系列答案
相关题目
1.a、b、c是三角形的三边长,且(a+b)2=c2+2ab,则这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
5.已知数349028用四舍五入法保留两个有效数字约是3.5×105,则所得近似数精确到( )
| A. | 十位 | B. | 千位 | C. | 万位 | D. | 百位 |
 如图所示,四边形ABCD是张大爷的一块小菜地,已知AD⊥AB,AD⊥CD,AD=$\sqrt{3}$,BC=CD=2$\sqrt{3}$,请帮张大爷计算一下这个四边形菜地的周长和面积.
如图所示,四边形ABCD是张大爷的一块小菜地,已知AD⊥AB,AD⊥CD,AD=$\sqrt{3}$,BC=CD=2$\sqrt{3}$,请帮张大爷计算一下这个四边形菜地的周长和面积.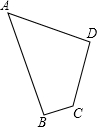 如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.