题目内容
15．
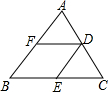如图，△ABC中，D是AC的中点，DF∥BC，交AB于F，DE∥AB，交BC于E，试判断：AF与DE，CE与DF的长度之间有什么关系？请说明理由．
分析 由三角形中位线判定定理得到DF、DE都是△ABC的中位线，然后三角形中位线的性质来判断AF与DE，CE与DF的长度之间的关系．
解答 解：AF=DE，CE=DF．理由如下：
∵D是AC的中点，DF∥BC，DE∥AB，
∴DF、DE都是△ABC的中位线，且四边形BEDF是平行四边形，
∴AF=BF，BE=EC，BF=DE，DF=BE，
∴AF=DE，CE=DF．
点评 本题考查了三角形中位线定理和平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．
练习册系列答案
相关题目
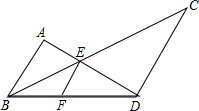如图，AB∥EF∥CD，E为AD与BC的交点，F在BD上，求证：$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$．
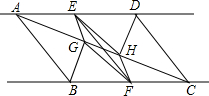如图，已知直线m∥n，A，D两点在直线m上，B，C两点在直线n上，且AB∥CD，E，F分别是AD，BC的中点，BG⊥AC，DH⊥AC，点G，H分别是垂足．求证：EF与GH互相平分．