题目内容
20. 如图,四边形ABCD是正方形,G是BC上的任意一点,BE⊥AG于E.BF⊥AG于点F.求证:AE-BE=EF.
如图,四边形ABCD是正方形,G是BC上的任意一点,BE⊥AG于E.BF⊥AG于点F.求证:AE-BE=EF.
分析 由ABCD是正方形,得到AB=DA、AB⊥AD,由BE⊥AG、DF⊥AG,结合题干得到∠ABE=∠DAF,于是得出△ABE≌△DAF,即可AF=BE.
解答 证明:∵ABCD是正方形,
∴AB=DA、AB⊥AD.
∵BE⊥AG、DF⊥AG,
∴∠AEB=∠AFD=90°,
又∵∠BAE+∠DAF=90°,∠BAE+∠ABE=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中,
$\left\{\begin{array}{l}{∠AEB=∠AFD}\\{∠ABE=∠AFD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△DAF(AAS),
∴AF=BE,
∴AE-BE=EF.
点评 本题主要考查正方形的性质,解答本题的关键是熟练掌握全等三角形的判定与性质定理,此题基础题,比较简单.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠A=60°,CD⊥AB于D,则AD=$\frac{1}{2}$AC=$\frac{1}{4}$AB,BC=2CD.
如图,在Rt△ABC中,∠A=60°,CD⊥AB于D,则AD=$\frac{1}{2}$AC=$\frac{1}{4}$AB,BC=2CD.
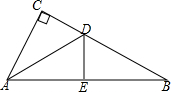 如图,△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,∠CDA=α,则∠B=2α-90°.
如图,△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,∠CDA=α,则∠B=2α-90°. 如图,在由边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠APD=$\frac{\sqrt{5}}{5}$.
如图,在由边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠APD=$\frac{\sqrt{5}}{5}$.
 如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D,求AB和AD的长.
如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D,求AB和AD的长.