Question

15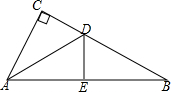．如图，△ABC中，∠C=90°，AC=AE，DE⊥AB于点E，∠CDA=α，则∠B=2α-90°．

Answer 1

分析 利用HL得到直角三角形ACD与直角三角形AED全等，利用全等三角形对应角相等得到∠ADC=∠ADE，求出∠CDE的度数，即可求出∠B的度数．

解答 解：∵DE⊥AB，
∴∠C=∠AED=90°，
在Rt△ACD和Rt△AED中，
$\left\{\begin{array}{l}{AD=AD}\\{AC=AE}\end{array}\right.$，
∴△ACD≌△AED（HL），
∴∠EDA=∠CDA=α，即∠CDE=2α，
则∠BDE=180°-2α，
∴∠B=90°-（180°-2α）=2α-90°．
故答案为：2α-90°

点评 此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．