题目内容
10. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.
每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.(1)画出△ABC关于点A旋转的△AB′C′,并写出A、B′、C′的坐标.
(2)求在旋转过程中,点B所经过的路径长.
分析 (1)分别作出点B、C绕点A逆时针旋转90°后得到的对应点即可得;
(2)根据弧长公式求解可得.
解答 解:(1)如图所示,△AB′C′即为所求;
A(1,-4)B(1,0)C(-2,-1);
(2)∵AB=4,∠BAB′=90°,
∴点B所经过的路径长为$\frac{90•π•4}{180}$=2π.
点评 本题主要考查图形的旋转及弧长的计算,熟练掌握旋转的定义和性质及弧长公式是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.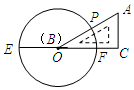 如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
 如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )| A. | 60≤x≤120 | B. | 30≤x≤60 | C. | 30≤x≤90 | D. | 30≤x≤120 |
19.一个角的余角和这个角的补角也互为补角,这个角的度数等于( )
| A. | 90° | B. | 75° | C. | 45° | D. | 15° |
20.在等边△ABC内部任取一点P,将△ABP绕点A旋转到△ACQ,则△APQ为( )
| A. | 不等腰的直角三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等边三角形 |
 将图中的△ABC作如下运动:
将图中的△ABC作如下运动: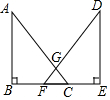 如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.