题目内容
在长方形纸片ABCD中,AB=1,BC=2,设E为边BC的中点,现将纸片折叠,使A、E重合,折痕将长方形纸片分为两部分,则较大部分面积与较小部分面积之比为多少?
考点:翻折变换(折叠问题)
专题:
分析:根据线段的中点的定义求出AE=BE=
,设折痕与AB的交点为F,根据折叠的性质求出AF,然后出BF,利用长方形的面积公式求出两个部分的面积,然后相比即可得解.
| 1 |
| 2 |
解答: 解:如图:
解:如图:
∵E为边BC的中点,
∴AE=BE=
AB=
,
设折痕与AB的交点为F,
由折叠的性质得,AF=EF=
AE=
×
=
,
∴BF=
+
=
,
又∵BC=2,
∴较大部分面积为
×2=
,
较小部分面积为
×2=
,
故较大部分面积与较小部分面积之比为3:1.
 解:如图:
解:如图:∵E为边BC的中点,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
设折痕与AB的交点为F,
由折叠的性质得,AF=EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴BF=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
又∵BC=2,
∴较大部分面积为
| 3 |
| 4 |
| 3 |
| 2 |
较小部分面积为
| 1 |
| 4 |
| 1 |
| 2 |
故较大部分面积与较小部分面积之比为3:1.
点评:本题考查了翻折变换,长方形的性质,熟记各性质并求出被折痕分成的两个长方形的宽是解题的关键.

练习册系列答案
相关题目
 某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图,请利用尺规作图找出音乐喷泉M的位置(要求:不写已知、求作、作法和结论,保留作图痕迹);连结AM、CM,则AM
某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图,请利用尺规作图找出音乐喷泉M的位置(要求:不写已知、求作、作法和结论,保留作图痕迹);连结AM、CM,则AM 如图,抛物线m=2与PEDF轴相交于A、B两点,与y轴相交于点C,顶点为D.
如图,抛物线m=2与PEDF轴相交于A、B两点,与y轴相交于点C,顶点为D.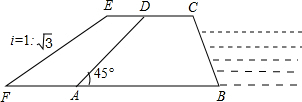 如图,某防洪指挥部发现长江边一处长600米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽2米,加固后背水坡EF的坡比i=1:
如图,某防洪指挥部发现长江边一处长600米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽2米,加固后背水坡EF的坡比i=1: