题目内容
16. 在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
分析 先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两角对应相等的两个三角形相似得到结论.
解答 证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°-∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
点评 本题考查了相似三角形的判定、等腰直角三角形的判定与性质;熟记有两角对应相等的两个三角形相似是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
6.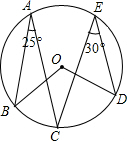 如图,在⊙O中,A、B、C、D均在圆上,∠BAC=25°,∠CED=30°,则∠BOD的度数是( )
如图,在⊙O中,A、B、C、D均在圆上,∠BAC=25°,∠CED=30°,则∠BOD的度数是( )
 如图,在⊙O中,A、B、C、D均在圆上,∠BAC=25°,∠CED=30°,则∠BOD的度数是( )
如图,在⊙O中,A、B、C、D均在圆上,∠BAC=25°,∠CED=30°,则∠BOD的度数是( )| A. | 55° | B. | 110° | C. | 125° | D. | 150° |
7.下列算式正确的是( )
| A. | 32=6 | B. | (-$\frac{1}{4}$)÷(-4)=1 | C. | (-8)2=-16 | D. | -5-(-2)=-3 |
4.若三角形的两边长分别为7和9,则第三边的长不可能是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
11.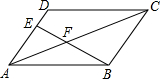 如图,在平行四边形ABCD中,点E在AD上,且DE:AE=1:2,连接BE,交AC于点F,则AF:AC=( )
如图,在平行四边形ABCD中,点E在AD上,且DE:AE=1:2,连接BE,交AC于点F,则AF:AC=( )
 如图,在平行四边形ABCD中,点E在AD上,且DE:AE=1:2,连接BE,交AC于点F,则AF:AC=( )
如图,在平行四边形ABCD中,点E在AD上,且DE:AE=1:2,连接BE,交AC于点F,则AF:AC=( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 2:5 |
5.抛物线y=-3(x+2)2-4的开口方向和对称轴分别是( )
| A. | 向上,x=2 | B. | 向上,x=-2 | C. | 向下,x=2 | D. | 向下,x-=2 |
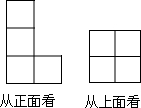 如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的.
如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的.