题目内容
已知四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线OB折叠,使点A落在D处,BD交OC于E.
(1)求OE的长;
(2)求过O、C、D三点抛物线的解析式;
(3)若F为过O、D、C三点抛物线的顶点,一动点P从点A出发,沿射线AB以每秒1个单位长度的速度匀速运动,当运动时间t秒为何值时,直线PF把△FOB分成面积之比为1:3的两部分?
(1)求OE的长;
(2)求过O、C、D三点抛物线的解析式;
(3)若F为过O、D、C三点抛物线的顶点,一动点P从点A出发,沿射线AB以每秒1个单位长度的速度匀速运动,当运动时间t秒为何值时,直线PF把△FOB分成面积之比为1:3的两部分?
考点:二次函数综合题
专题:
分析:(1)先根据AAS定理得出△BEC≌△OED,再根据勾股定理求出OE的长;
(2)过D作DG⊥OC于G,可得出△ODE∽△OGD,根据相似三角形的性质求出CD两点的坐标,利用待定系数法求出抛物线的解析式即可;
(3)先求出直线OB的解析式为y=
x,设直线PF交OB于H,H(m,
m),过H作HM⊥OA垂足为M,则△oMH∽△oab,根据相似三角形的对应边成比例求出HM的长、OM的长,求得H的坐标,然后根据F、H的坐标求得直线PF的解析式,进而可得出结论;
(2)过D作DG⊥OC于G,可得出△ODE∽△OGD,根据相似三角形的性质求出CD两点的坐标,利用待定系数法求出抛物线的解析式即可;
(3)先求出直线OB的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)如图1,∵四边形OABC为矩形,△OBD是由△OAB沿BD翻折而成,且A(0,4),B(8,4),C(0,8),则OD=BC=OA=4,
解:(1)如图1,∵四边形OABC为矩形,△OBD是由△OAB沿BD翻折而成,且A(0,4),B(8,4),C(0,8),则OD=BC=OA=4,
∠D=∠ECB=90°,∠OED=∠BEC,
∵
,
∴△OED≌△BEC(AAS),
∴DE=EC,
设OE=x,则EC=8-x,
∴x2=(8-x)2+42.
∴OE=5,
(2)如图2,过D作DG⊥OC于G,故△ODE∽△OGD,
∵OE=5,
∴DE=EC=8-5=3,
∴
=
=
,
即
=
=
,解得,DG=
,OG=
,
∴D(
,-
),
由于过点O、D、C的抛物线经过原点,则设y=ax2+bx,而C(8,0),D(
,-
),
∴
,
解之得
,
∴y=
x2-
x;
(3)如图3,由y=
x2-
x;
=
(x2-8x+16)-
=
(x-4)2-
,
故顶点F的坐标为F(4,-
);
易求直线OB的解析式为yOB=
x,设直线PF交OB于H,H(m,
m),
过H作HM⊥OA垂足为M,则△OMH∽△OAB,
∵直线PF把△FOB分成面积之比为1:3的两部分,
∴
=
或
=
∴
=
=
或
=
∴OM=
×4=1或OM=
×4=3
∴MH=2或MH=6,
∴HM=2或6,而m=2或6,
∴H1(2,1),H2(6,3),
∴直线FH1的解析式为y=-
x+
,当y=4时,x=
,
直线EH2的解析式为y=
x-
,当y=4时,x=
,
故当t=
秒或
秒,直线PF把△FOB分成面积之比为1:3的两部分.
 解:(1)如图1,∵四边形OABC为矩形,△OBD是由△OAB沿BD翻折而成,且A(0,4),B(8,4),C(0,8),则OD=BC=OA=4,
解:(1)如图1,∵四边形OABC为矩形,△OBD是由△OAB沿BD翻折而成,且A(0,4),B(8,4),C(0,8),则OD=BC=OA=4,∠D=∠ECB=90°,∠OED=∠BEC,
∵
|
∴△OED≌△BEC(AAS),
∴DE=EC,
设OE=x,则EC=8-x,
∴x2=(8-x)2+42.
∴OE=5,
(2)如图2,过D作DG⊥OC于G,故△ODE∽△OGD,
∵OE=5,

∴DE=EC=8-5=3,
∴
| OD |
| OE |
| DG |
| DE |
| OG |
| OD |
即
| 4 |
| 5 |
| DG |
| 3 |
| OG |
| 4 |
| 12 |
| 5 |
| 16 |
| 5 |
∴D(
| 16 |
| 5 |
| 12 |
| 5 |
由于过点O、D、C的抛物线经过原点,则设y=ax2+bx,而C(8,0),D(
| 16 |
| 5 |
| 12 |
| 5 |
∴
|
解之得
|
∴y=
| 5 |
| 32 |
| 5 |
| 4 |
(3)如图3,由y=
| 5 |
| 32 |
| 5 |
| 4 |
=
| 5 |
| 32 |
| 5 |
| 2 |
| 5 |
| 32 |
| 5 |
| 2 |

故顶点F的坐标为F(4,-
| 5 |
| 2 |
易求直线OB的解析式为yOB=
| 1 |
| 2 |
| 1 |
| 2 |
过H作HM⊥OA垂足为M,则△OMH∽△OAB,
∵直线PF把△FOB分成面积之比为1:3的两部分,
∴
| OH |
| OB |
| 1 |
| 4 |
| OH |
| OB |
| 3 |
| 4 |
∴
| OH |
| OB |
| OM |
| OA |
| 1 |
| 4 |
| OM |
| OA |
| 3 |
| 4 |
∴OM=
| 1 |
| 4 |
| 3 |
| 4 |
∴MH=2或MH=6,
∴HM=2或6,而m=2或6,
∴H1(2,1),H2(6,3),
∴直线FH1的解析式为y=-
| 7 |
| 4 |
| 9 |
| 2 |
| 2 |
| 7 |
直线EH2的解析式为y=
| 11 |
| 4 |
| 27 |
| 2 |
| 70 |
| 11 |
故当t=
| 2 |
| 7 |
| 70 |
| 11 |
点评:本题考查的是一次函数综合题,涉及到利用待定系数法求一次函数及二次函数的解析式、全等三角形及相似三角形的判定与性质,难度较大.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若a=-4b,则对a的任何值多项式a2+3ab-4b2+2的值( )
| A、总是2 | B、总是0 |
| C、总是1 | D、是不确定的值 |
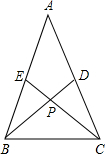 如图,在△ABC中,D、E分别为AC、AB的中点,
如图,在△ABC中,D、E分别为AC、AB的中点,
 如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.
如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.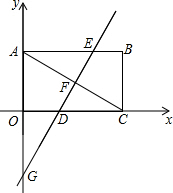 如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30° 如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花
如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花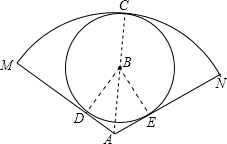 如图,∠MAN=120°,⊙B的半径为r,⊙B与
如图,∠MAN=120°,⊙B的半径为r,⊙B与