题目内容
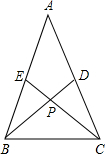
在△ABC中,∠C=60°,AD,BE是高,AD、BE相交于O点,连接DE,求证:DE=
AB.
| 1 |
| 2 |
考点:含30度角的直角三角形
专题:
分析:解直角三角形求出
=
=
,再根据图形得出∠C=∠C,推出△CDE∽△CAB,得出比例式,即可得出答案.
| CD |
| AC |
| CE |
| BC |
| 1 |
| 2 |
解答: 证明:∵AD,BE是高,
证明:∵AD,BE是高,
∴∠ADC=∠BEC=90°,
∵∠C=60°,
∴cos60°=
=
=
,
∵∠C=∠C,
∴△CDE∽△CAB,
∴
=
=
,
∴DE=
AB.
 证明:∵AD,BE是高,
证明:∵AD,BE是高,∴∠ADC=∠BEC=90°,
∵∠C=60°,
∴cos60°=
| CD |
| AC |
| CE |
| BC |
| 1 |
| 2 |
∵∠C=∠C,
∴△CDE∽△CAB,
∴
| CD |
| AC |
| DE |
| AB |
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
点评:本题考查了解直角三角形,特殊角的三角函数值,相似三角形的性质和判定的应用,解此题的关键是推出△CDE∽△CAB.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
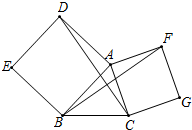 如图,以△ABC中AB、AC为边分别作正方形ADEB与ACGF,连接DC、BF.则CD与BF的数量关系是
如图,以△ABC中AB、AC为边分别作正方形ADEB与ACGF,连接DC、BF.则CD与BF的数量关系是
 如图,在△ABC中,D、E分别为AC、AB的中点,
如图,在△ABC中,D、E分别为AC、AB的中点, 如图的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率等于
如图的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率等于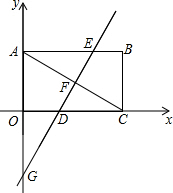 如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°