Question

11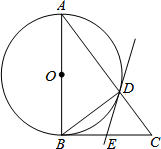．如图，在△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D的直线交BC边于点E，∠BDE=∠A．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径R=5，cosA=$\frac{4}{5}$，求线段CD的长．

Answer 1

分析 （1）连接OD，利用圆周角定理以及等腰三角形的性质得出OD⊥DE，进而得出答案；
（2）在Rt△ABC中根据AC=$\frac{AB}{cosA}$求得AC，在RT△ABD中由AD=ABcosA求得AD，即可得答案．

解答 解：（1）直线DE与⊙O相切．
理由如下：连接OD．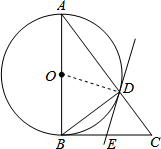

∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切；

（2））∵R=5，
∴AB=10，
在Rt△ABC中
∵cosA=$\frac{AB}{AC}$=$\frac{4}{5}$
∴AC=$\frac{AB}{cosA}$=$\frac{10}{\frac{4}{5}}$=$\frac{25}{2}$，
又∵在RT△ABD中，AD=ABcosA=10×$\frac{4}{5}$=8，
∴CD=AC-AD=$\frac{25}{2}$-8=$\frac{9}{2}$．

点评 此题主要考查了切线的判定和圆周角定理及三角函数的应用等知识，熟练掌握圆周角定理与切线的判定是解题的关键．