题目内容
16.已知双曲线y=-$\frac{4}{x}$上一点P的横坐标为-$\frac{2}{3}$,P点关于y轴的对称点是Q,双曲线y=$\frac{k}{x}$经过点Q.(1)求y=$\frac{k}{x}$的表达式;
(2)说出双曲线y=$\frac{k}{x}$所在的象限以及在每个象限内y随x值的增大而变化的情况.
分析 (1)把P横坐标代入已知双曲线解析式求出纵坐标,确定出P坐标,进而求出Q坐标,代入反比例解析式求出k的值,即可求出反比例解析式;
(2)利用反比例函数性质判断即可.
解答 解:(1)∵点P在双曲线y=-$\frac{4}{x}$上,
∴把x=-$\frac{2}{3}$代入得:y=6,即P(-$\frac{2}{3}$,6),
∵P与Q关于y轴对称,
∴Q($\frac{2}{3}$,6),
代入y=$\frac{k}{x}$中得:k=4,
则反比例解析式为y=$\frac{4}{x}$;
(2)∵y=$\frac{4}{x}$,且k=4>0,
∴此函数的图象在第一、三象限,在每个象限内y随x的增大而减小.
点评 此题考查了待定系数法求反比例函数解析式,以及反比例函数图象上点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
 如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )| A. | y=$\frac{3}{4}$x | B. | y=$\frac{2}{3}$x | C. | y=$\frac{4}{3}$x | D. | y=$\frac{5}{6}$x |

 如图,已知⊙O中,AB是直径,PA和PC分别与⊙O相切于A,C两点,连结OP,CB
如图,已知⊙O中,AB是直径,PA和PC分别与⊙O相切于A,C两点,连结OP,CB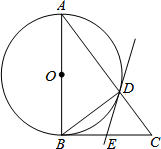 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A. 如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).
如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0). 如图,在直角坐标平面内,Rt△AOB中,点A(1,0),OB=2,将△AOB绕点A顺时针旋转90°后与△ACD重合,点O、B分别与点C、D对应,求点D的坐标.
如图,在直角坐标平面内,Rt△AOB中,点A(1,0),OB=2,将△AOB绕点A顺时针旋转90°后与△ACD重合,点O、B分别与点C、D对应,求点D的坐标.