题目内容
1. 如图,将长方形ABCD沿对角线BD折叠,点C落在点C′处,若AB=2,则C′D的长是2.
如图,将长方形ABCD沿对角线BD折叠,点C落在点C′处,若AB=2,则C′D的长是2.
分析 根据矩形的性质可得AB=CD=2,再根据折叠可得C′D=CD=2.
解答 解:∵四边形ABCD是矩形,
∴AB=CD,
∵AB=2,
∴CD=2,
∵长方形ABCD沿对角线BD折叠,点C落在点C′处,
∴C′D=CD=2,
故答案为:2.
点评 此题主要考查了矩形的性质和翻折变换,关键是找准折叠后哪些线段是对应相等的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | 种型号 | ||
| 第一周 | 3台 | 4台 | 1200元 |
| 第二周 | 5台 | 6台 | 1900元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
6. 如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
 如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )| A. | y=$\frac{3}{4}$x | B. | y=$\frac{2}{3}$x | C. | y=$\frac{4}{3}$x | D. | y=$\frac{5}{6}$x |
13. 某公司服装营业人员5月份的销售情况如表:
某公司服装营业人员5月份的销售情况如表:
(1)指出这组销售数据的众数和中位数;
(2)计算这组销售数据的平均数;
(3)补全图中的条形统计图.
 某公司服装营业人员5月份的销售情况如表:
某公司服装营业人员5月份的销售情况如表:| 销售额/万元 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 23 | 24 |
| 人数 | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 | 1 |
(2)计算这组销售数据的平均数;
(3)补全图中的条形统计图.
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
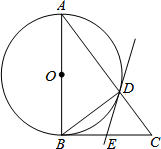 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A. 如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.
如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.
