题目内容
2.已知a,b,c满足|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2=2+2ac,则a-b+c的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 因为a,b,c满足|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2=2+2ac,则这个等式必须有意义,则 $\sqrt{(a-3){b}^{2}}$必有意义,从而确定a的取值,然后将a的值代入等式
|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2,分析等式的特征并确定b、c的值即可
解答 解:∵已知a,b,c满足|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2=2+2ac,
∴|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2,…①
且$\sqrt{(a-3){b}^{2}}$必有意义,
又∵b2≥0,
∴a-3≥0
①当a-3>0时,|2a-4|>2,
有|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac>2,
则这与①式相矛盾,即a-3>0不成立;
②当a-3=0时,a=3,则
|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2+|b+2|+0+(c-3)2=2,
|b+2|+(c-3)2=0,
又∵|b+2|≥0,(c-3)2≥0,
∴必有b+2=0,c-3=0
即:b=-2,c=3
∴a-b+c=3-(-2)+3=8
故:选D
点评 本题考查了二次根式有意义的条件、配方法的应用、几个非负数的和为零的条件等知识点;解题的关键是根据条件中等式的特点及二次根式有意义的条件确定a、b、的取值c

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
20.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 25 | 29 | 32 | 34 | 35 | 38 | 40 |
| 人数(人) | 2 | 4 | 3 | 7 | 9 | 7 | 6 |
| A. | 该班一共有38名同学 | |
| B. | 该班学生这次考试成绩的众数是35分 | |
| C. | 该班学生这次考试成绩的中位数是35分 | |
| D. | 该班学生这次考试成绩的平均数是35分 |
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,等腰直角△POA的直角顶点P在反比例函数$y=\frac{4}{x}$(x>0)的图象上,A点在x轴正半轴上,求A点坐标.
如图,等腰直角△POA的直角顶点P在反比例函数$y=\frac{4}{x}$(x>0)的图象上,A点在x轴正半轴上,求A点坐标. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=4.5.
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=4.5.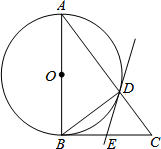 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A. 如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.
如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.