题目内容
6. 如图,C是以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C是以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.(1)求证:AC平分∠BAD;
(2)若CD=3,tan∠DAC=$\frac{1}{2}$,求⊙O的直径.
分析 (1)如图连接OC,只要证明∠DAC=∠ACO,∠ACO=∠CAB即可.
(2)连接BC,只要证明△ADC∽△ACB,得$\frac{AD}{AC}$=$\frac{AC}{AB}$,再求出AD、AC即可解决问题.
解答 (1)证明:如图连接OC,
∵CD切⊙O于点C,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAB,
∴∠DAC=∠CAB,
∴AC平分∠BAD.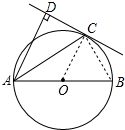
(2)如图连接BC.
∵AB是⊙O直径,
∴∠ACB=90°,
∵AD⊥CD,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∵tan∠ADC=$\frac{CD}{AD}$=$\frac{1}{2}$,CD=3,
∴AD=6,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴$\frac{6}{3\sqrt{5}}$=$\frac{3\sqrt{5}}{AB}$,
∴AB=$\frac{15}{2}$,即⊙O的直径为$\frac{15}{2}$.
点评 本题考查切线的性质、角平分线的性质、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形,属于中考常考题型.

练习册系列答案
相关题目
20.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 25 | 29 | 32 | 34 | 35 | 38 | 40 |
| 人数(人) | 2 | 4 | 3 | 7 | 9 | 7 | 6 |
| A. | 该班一共有38名同学 | |
| B. | 该班学生这次考试成绩的众数是35分 | |
| C. | 该班学生这次考试成绩的中位数是35分 | |
| D. | 该班学生这次考试成绩的平均数是35分 |
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
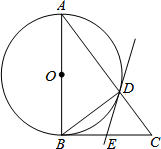 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.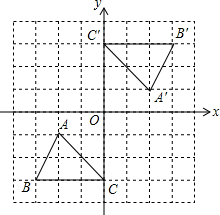 如图,已知格点△ABC和△A′B′C′关于原点O成中心对称,在方格网中确定一点D,使以A,O,C′,D为顶点的四边形是平行四边形,则点D的坐标为(2,4)或(-2,-4)或(-2,2)(请写出所有满足条件的点D的坐标)
如图,已知格点△ABC和△A′B′C′关于原点O成中心对称,在方格网中确定一点D,使以A,O,C′,D为顶点的四边形是平行四边形,则点D的坐标为(2,4)或(-2,-4)或(-2,2)(请写出所有满足条件的点D的坐标)
