题目内容
抛物线最高点坐标(
,0),形状与抛物线y=1+3x2相同,则抛物线的解析式为 .
| 3 |
| 2 |
考点:二次函数图象与几何变换
专题:几何变换
分析:由于已知抛物线的顶点坐标,则设顶点式y=a(x-
)2,然后根据二次函数的性质求出a的值即可.
| 3 |
| 2 |
解答:解:设抛物线解析式为y=a(x-
)2,
∵所求抛物线与抛物线y=1+3x2相同,
∴a=3,
∴所求抛物线解析式为y=3(x-
)2.
故答案为y=3(x-
)2.
| 3 |
| 2 |
∵所求抛物线与抛物线y=1+3x2相同,
∴a=3,
∴所求抛物线解析式为y=3(x-
| 3 |
| 2 |
故答案为y=3(x-
| 3 |
| 2 |
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.也考查了二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由. 如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明.
如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明.
 在方框内填上正确的数.
在方框内填上正确的数. 如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.
如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.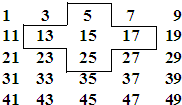 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.