题目内容
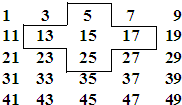 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.(1)计算十字框中的五个数的和,并说明与中间数15有什么关系?若将十字框中上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?
(2)设中间数为a,用式子表示十字框中五个数分别是多少?并求出这五个数之和;
(3)十字框中五个数之和能等于2000吗?若能,请写出这五个数;若不能,说明理由.
考点:一元一次方程的应用
专题:规律型
分析:(1)先求出这5个数的和,用这个和去除以中间的这个数15就可以得出结论;
(2)由左右相邻两个奇数之间相差2,上下相邻两个奇数之间相差10,就可以分别表示出这5个数,进而得出结论;
(3)设中间的一个数为x,建立方程求出x的值就可以得出结论.
(2)由左右相邻两个奇数之间相差2,上下相邻两个奇数之间相差10,就可以分别表示出这5个数,进而得出结论;
(3)设中间的一个数为x,建立方程求出x的值就可以得出结论.
解答:解:(1)由题意,得
5+13+15+17+25=75.
75÷15=5.
故十字框中的五个数的和是中间数15的5倍;
设中间数为b,则其余的4个数分别为b-2,b+2,b-10,b+10,由题意,得
∵b+b-2+b+2+b-10+b+10=5b,
∴这五个数的和还是中间这个数的5倍;
(2)设中间数为a,则其余的4个数分别为a-2,a+2,a-10,a+10,由题意,得
a+a-2+a+2+a-10+a+10=5a.
答:5个数之和为5a;
(3)设中间的一个数为x,则其余的4个数分别为x-2,x+2,x-10,x+10,由题意,得
x+x-2+x+2+x-10+x+10=2000,
解得:x=400.
∵400是偶数,
∴不存在十字框中五数之和等于2000.
5+13+15+17+25=75.
75÷15=5.
故十字框中的五个数的和是中间数15的5倍;
设中间数为b,则其余的4个数分别为b-2,b+2,b-10,b+10,由题意,得
∵b+b-2+b+2+b-10+b+10=5b,
∴这五个数的和还是中间这个数的5倍;
(2)设中间数为a,则其余的4个数分别为a-2,a+2,a-10,a+10,由题意,得
a+a-2+a+2+a-10+a+10=5a.
答:5个数之和为5a;
(3)设中间的一个数为x,则其余的4个数分别为x-2,x+2,x-10,x+10,由题意,得
x+x-2+x+2+x-10+x+10=2000,
解得:x=400.
∵400是偶数,
∴不存在十字框中五数之和等于2000.
点评:本题考查了数的倍数的运用,列一元一次方程解实际问题的运用,一元一次方程的解法的运用,代数式的运用,解答时根据5x=2000建立方程是关键.

练习册系列答案
相关题目
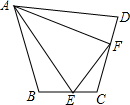 如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=
如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=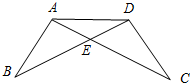 在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式: 在如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若C也是图中的格点,且使得△ABC为等腰三角形,在网格中画出所有符合条件的点C.
在如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若C也是图中的格点,且使得△ABC为等腰三角形,在网格中画出所有符合条件的点C.